
����Ŀ����ͼ1������ABCD��һ��BC��ֱ������ϵ��x���ϣ��۵���AD��ʹ��D����x���ϵ�F�����ۺ�ΪAE����֪AB��8��AD��10�������B����Ϊ��m��0��������m��0��
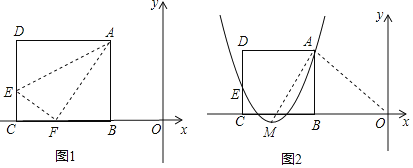
��1�����E��F�����꣨�ú�m��ʽ�ӱ�ʾ����
��2������OA������OAF�ǵ��������Σ���m��ֵ��
��3����ͼ2����������y��a��x��m+6��2+h����A��E���㣬�䶥��ΪM������AM������OAM��90������a��h��m��ֵ��
���𰸡���1����E������Ϊ��m��10��3������F������Ϊ��m��6��0������2��m����6��4��![]() ����3��a��
����3��a��![]() ��h����1��m����12
��h����1��m����12
��������
��1�������ı���ABCD�Ǿ����Լ����۵��Գ��Եó�AF=AD=10��EF=DE���������BF�ij������ɵó�E��F������ꣻ
��2��������������ۣ���AO=AF��OF=FA��AO=OF�����õ������������ʺ��ɶ���������ɣ�
��3����E��m+10��3����A��m��8����������κ�������ʽ�ó�M������꣬��֤��AOB�ס�AMG�������������������ʿ����m��ֵ���ɣ�
�⣺��1�����ı���ABCD�Ǿ��Σ�AB��8��AD��10��
��AD��BC��10��AB��CD��8����D����DCB����ABC��90����
���۵��Գ��ԣ�AF��AD��10��FE��DE��
��Rt��ABF��BF��![]() ��6��
��6��
��FC��4��
��DE��x����CE��8��x��
��Rt��ECF��42+��8��x��2��x2����x��5��
��CE��8��x��3��
�ߵ�B������Ϊ��m��0����
���E��������m��10��3������F��������m��6��0����
��2���������������ۣ�
��AO��AF��
��AB��OF��BF��6��
��OB��BF��6��
��m����6��
��OF��AF����m��6����10����m����4��
��AO��OF��
��Rt��AOB��AO2��OB2+AB2��m2+64��
�ࣨm��6��2��m2+64����m����![]() ��
��
���Ͽɵã�m����6��4��![]() ��
��
��3���ɣ�1��֪A��m��8����E��m��10��3����
��������y��a��x��m+6��2+h����A��E���㣬
��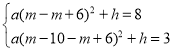 ��
��
��ã�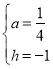 ��
��
��������ߵĽ���ʽΪy��![]() ��x��m+6��2��1��
��x��m+6��2��1��
���M��������m��6����1����
��Գ��ύAD��G��
��G��m��6��8����
��AG��6��GM��8������1����9��
�ߡ�OAB+��BAM��90������BAM+��MAG��90����
���OAB����MAG��
�֡ߡ�ABO����MGA��90����
���AOB�ס�AMG��
��![]() ��
��
��![]() ��
��
��ã�m����12��
���Ͽɵã�a��![]() ��h����1��m����12��
��h����1��m����12��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O��ֱ��AB��26��P��AB��(�����A��B�غ�)����һ�㣬��C��DΪ��O�ϵ����㣬����APD����BPC����ơ�CPDΪֱ��AB�ġ������ǡ���
(1)����BPC����DPC��60�㣬���CPD��ֱ��AB�ġ������ǡ��𣿲�˵�����ɣ�
(2)��![]() �ij�Ϊ
�ij�Ϊ![]() ���������ǡ���CPD�Ķ�����
���������ǡ���CPD�Ķ�����
(3)��ֱ��AB�ġ������ǡ�Ϊ120�㣬�ҡ�PCD���ܳ�Ϊ24+13![]() ��ֱ��д��AP�ij���
��ֱ��д��AP�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
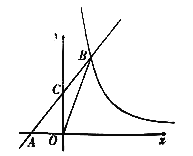
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�ֱ��y=kx+b(k��0)���ύ�ڵ�A(-2.0)���뷴��������y=![]() (m��0)��ͼ���ڵ�B(2,n)������BO����S��AOB=4.
(m��0)��ͼ���ڵ�B(2,n)������BO����S��AOB=4.
(1)����������һ�κ����ı���ʽ:
(2)��ֱ��AB��y��Ľ���ΪC.���OCB�����
(3)����ͼ��ֱ��д����x>0ʱ,����ʽ![]() >kx+b�Ľ⼯��
>kx+b�Ľ⼯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
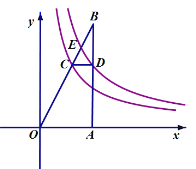
����Ŀ����ͼ��![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() ��������ᣬ
��������ᣬ![]() ��
��![]() �ֱ���˫����
�ֱ���˫����![]()
![]() ��
��![]()
![]() �ཻ�ڵ�
�ཻ�ڵ�![]() �͵�
�͵�![]() ����
����![]() ����
����![]() �����
�����![]() �ĺ�����Ϊ�� ��
�ĺ�����Ϊ�� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ķ��ദ����������ã����Լ�����Ⱦ����ʡ��Դ��ij���л�������Ϊ���������ʵЧ�����������˲��־���С��һ��ʱ�������������ķ���������������Ϣ���£�

����ͼ������������⣺
��1���뽫����ͳ��ͼ����������
��2��������ͳ��ͼ���У��������к�����C����Ӧ��Բ�Ľ� �ȣ�
��3�����鷢�֣��ڿɻ�����������������ռ13%��ÿ����1�������������ɻ��0.5�ֶ���ԭ�ϣ�����ó���ÿ�²�������������Ϊ1000�֣���ȫ�����ദ������ôÿ�»��յ��������������Ի�ö��ٶֶ���ԭ�ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB��90������D��AB�ϣ���ADΪֱ���ġ�O���BC�����ڵ�E�����AC�ཻ�ڵ�G����![]() ������GO���ӳ�����O�ڵ�F������BF��
������GO���ӳ�����O�ڵ�F������BF��
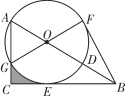
��1����֤��AO��AG��
��2����֤��BF�ǡ�O�����ߣ�
��3����BD��6����ͼ������Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
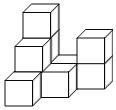
����Ŀ����ͼ����һ����ѧ����ϣ�������10���߳�Ϊ1��С�����δ����һ�������壬Ȼ����������������ͬ����С���������Ա��ٴ�һ�������壬ʹ�����������ǡ�ÿ��Ժ������������ƴ��һ����϶�Ĵ��壨���ı���������������״������ô�������ٻ���Ҫ______��С�����壬�����������ı����Ϊ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ���꼶��1��������ѧ���μ�2010����б�ҵ����ѧ�������ԣ����ݲ������ֱ��������ǵijɼ�����ͳ�ƺ��ΪA��B��C��D�ĵȣ������Ƴ���ͼ��ʾ������ͳ��ͼ������ͳ��ͼ��δ��ɣ�������ͼ��������Ϣ����������⣺
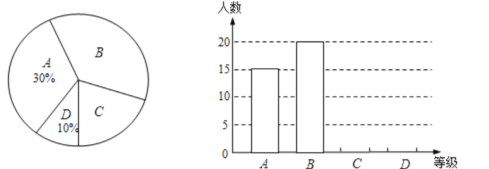
�� ���꼶��1����μ��������Ե�ѧ����_________�ˣ�
�� ������ͳ��ͼ����������
�� ������ͳ��ͼ�У��ȼ�B������ռ�İٷֱ���___���ȼ�C��Ӧ��Բ�ĽǵĶ���Ϊ___����
�� ����У���꼶ѧ������850�˲μ��������ԣ����ƴﵽA����B����ѧ������___�ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס������˼ӹ�ͬһ���������ÿ��ӹ�����������ÿ��ӹ�������1.5�������˸��ӹ�300������������ױ�������5�죮
��1����ס�������ÿ����ӹ����ٸ����������
��2����֪�ס������˼ӹ��������ÿ��ļӹ��ѷֱ���150Ԫ��120Ԫ������1500����������ļӹ��������ӹ�һ��ʱ������а��ţ�ʣ���������ҵ�����ɣ�����ܼӹ���Ϊ7800Ԫ����ô�ס��Ҹ��ӹ��˶����죿
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com