
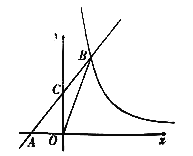
【题目】如图,在平面直角坐标系xOy中,直线y=kx+b(k≠0)与轴交于点A(-2.0),与反比例函数y=![]() (m≠0)的图象交于点B(2,n),连接BO,若S△AOB=4.
(m≠0)的图象交于点B(2,n),连接BO,若S△AOB=4.
(1)求反比例函数和一次函数的表达式:
(2)若直线AB与y轴的交点为C.求△OCB的面积
(3)根据图象,直接写出当x>0时,不等式![]() >kx+b的解集.
>kx+b的解集.
【答案】(1)y=![]() ,y=x+2;(2)S△OCB=2;(3)0<x<2.
,y=x+2;(2)S△OCB=2;(3)0<x<2.
【解析】
|(1)先由A(-2,0),得OA=2,点B(2,n),S△AOB=4,得![]() OAn=4,n=4,则点B的坐标是(2,4),把点B(2,4)代入反比例函数的解析式为y=
OAn=4,n=4,则点B的坐标是(2,4),把点B(2,4)代入反比例函数的解析式为y=![]() ,可得反比例函数的解析式为:y=
,可得反比例函数的解析式为:y=![]() ;再把A(-2,0)、B(2,4)代入直线AB的解析式为y=kx+b可得直线AB的解析式为y=x+2;
;再把A(-2,0)、B(2,4)代入直线AB的解析式为y=kx+b可得直线AB的解析式为y=x+2;
(2)把x=0代入直线AB的解析式y=x+2得y=2,即OC=2,可得S△OCB=![]() OC×2=
OC×2=![]() ×2×2=2;
×2×2=2;
(3)根据图象,可知不等式![]() >kx+b的解集0<x<2.
>kx+b的解集0<x<2.
解:(1)由A(-2,0),得OA=2;
∵点B(2,n)在第一象限内,S△AOB=4,
∴![]() OAn=4;
OAn=4;
∴n=4;
∴点B的坐标是(2,4);
将点B的坐标(2,4)代入反比例函数![]() ,得
,得![]() ,
,
∴m=8;
∴反比例函数的解析式为:y=![]() ;
;
将点A(2,0),B(2,4)的坐标分别代入y=kx+b,得 ![]() ,
,
解得![]() ;
;
∴一次函数的表达式y=x+2.
(2)在y=x+2中,令x=0,得y=2,
∴点C的坐标是(0,2),
∴OC=2,
∴S△OCB=![]() ×2×2=2.
×2×2=2.
(3)由于B点坐标为(2,4),可知不等式![]() 的解集0<x<2.
的解集0<x<2.
故答案为(1)y=![]() ,y=x+2;(2)S△OCB=2;(3)0<x<2.
,y=x+2;(2)S△OCB=2;(3)0<x<2.


 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
【题目】已知![]() 内接于圆
内接于圆![]() ,点
,点![]() 为弧
为弧![]() 上一点,连接
上一点,连接![]() 交
交![]() 于点
于点![]() ,
,![]() .
.
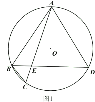
(1)如图1,求证:弧![]() 弧
弧![]() ;
;
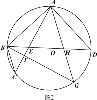
(2)如图2,过![]() 作
作![]() 于点
于点![]() ,交圆
,交圆![]() 点
点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,且
,且![]() ,求
,求![]() 的度数;
的度数;
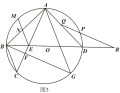
(3)如图3,在(2)的条件下,圆![]() 上一点
上一点![]() 与点
与点![]() 关于
关于![]() 对称,连接
对称,连接![]() ,交
,交![]() 于点
于点![]() ,点
,点![]() 为弧
为弧![]() 上一点,
上一点,![]() 交
交![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,
,![]() ,
,![]() 的周长为20,
的周长为20,![]() ,求圆
,求圆![]() 半径.
半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图甲,在四边形ABCD中,AD//BC,∠C=90°动点P从点C出发沿线段CD向点D运动.到达点D即停止,若E、F分别是AP、BP的中点,设CP=x,△PEF的面积为y,且y与x之间的函数关系的图象如图乙所示,则线段AB长为( )
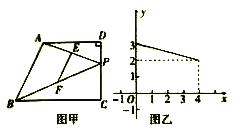
A.2![]() B.2
B.2![]() C.2
C.2![]() D.2
D.2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个摩天轮,它共有8个座舱,依次标为1~8号,摩天轮中心O的离地高度为50米,摩天轮中心到各座舱中心均相距25米,在运行过程中,当1号舱比3号舱高5米时,1号舱的离地高度为_____米.
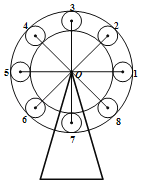
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了美化环境,建设宜居成都,我市准备在一个广场上种植甲、乙两种花卉,进市场调查,甲种花卉的种植费用y(元)与种植面积xm2之间的函数关系如图所示,乙种花卉的种植费用为100元/m2.
(1)请直接写出当0≤x≤300和x>300时,y与x的函数关系式;

(2)广场上甲、乙两种花卉的种植面积共1200m2,如果甲种花卉的种植面积不少于200m2,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植总费用最少?最少总费用为多少元?
(3)在(2)的条件下,若种植总费用不小于123000元,求出甲种花卉种植面积的范围是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,矩形ABCD的一边BC在直角坐标系中x轴上,折叠边AD,使点D落在x轴上点F处,折痕为AE,已知AB=8,AD=10,并设点B坐标为(m,0),其中m<0.
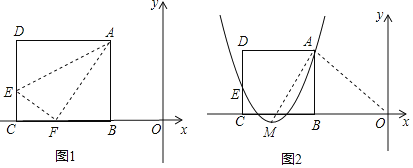
(1)求点E、F的坐标(用含m的式子表示);
(2)连接OA,若△OAF是等腰三角形,求m的值;
(3)如图2,设抛物线y=a(x﹣m+6)2+h经过A、E两点,其顶点为M,连接AM,若∠OAM=90°,求a、h、m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在同一直角坐标系xOy中,有双曲线![]() ,直线y2=k2x+b1,y3=k3x+b2,且点A(2,5),点B(﹣6,n)在双曲线的图象上
,直线y2=k2x+b1,y3=k3x+b2,且点A(2,5),点B(﹣6,n)在双曲线的图象上
(1)求y1和y2的解析式;
(2)若y3与直线x=4交于双曲线,且y3∥y2,求y3的解析式;
(3)直接写出![]() 的解集.
的解集.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com