
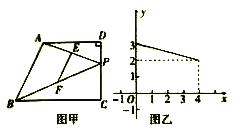
【题目】如图甲,在四边形ABCD中,AD//BC,∠C=90°动点P从点C出发沿线段CD向点D运动.到达点D即停止,若E、F分别是AP、BP的中点,设CP=x,△PEF的面积为y,且y与x之间的函数关系的图象如图乙所示,则线段AB长为( )
A.2![]() B.2
B.2![]() C.2
C.2![]() D.2
D.2![]()
【答案】C
【解析】
根据三角形中位线定理,得到S△PEF=![]() S△ABP,由图像可以看出当x为最大值CD=4时,S△PEF=2,可求出AD=4,当x为0时,S△PEF=3,可求出BC=6;过点A作AG⊥BC于点G,根据勾股定理即可得解.
S△ABP,由图像可以看出当x为最大值CD=4时,S△PEF=2,可求出AD=4,当x为0时,S△PEF=3,可求出BC=6;过点A作AG⊥BC于点G,根据勾股定理即可得解.
解:∵E、F分别为AP、BP的中点,
∴EF∥AB,EF=![]() AB,
AB,
∴S△PEF=![]() S△ABP,
S△ABP,
根据图像可以看出x的最大值为4,
∴CD=4,
∵当P在D点时,△PEF的面积为2,
∴S△ABP=2×4=8,即S△ABD=8,
∴AD=![]() =
=![]() =4,
=4,
当点P在C点时,S△PEF=3,
∴S△ABP=3×4=12,即S△ABC=12,
∴BC=![]() =
=![]() =6,
=6,
过点A作AG⊥BC于点G,
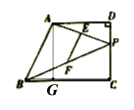
∴∠AGC=90°,
∵AD∥BC,
∴∠ADC+∠BCD=180°,
∵∠BCD=90°,
∴∠ADC=180°-90°=90°,
∴四边形AGCD是矩形,
∴CG=AD=4,AG=CD=4,
∴BG=BC-CG=6-4=2,
∴AB=![]() =2
=2![]() .
.
故选C.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为F,连接DE.
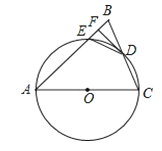
(1)求证:直线DF与⊙O相切;
(2)若AE=7,BC=6,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明对函数![]() 的图象和性质进行了探究.已知当自变量
的图象和性质进行了探究.已知当自变量![]() 的值为
的值为![]() 或
或![]() 时,函数值都为
时,函数值都为![]() ;当自变量
;当自变量![]() 的值为
的值为![]() 或
或![]() 时,函数值都为
时,函数值都为![]() .探究过程如下,请补充完整.
.探究过程如下,请补充完整.
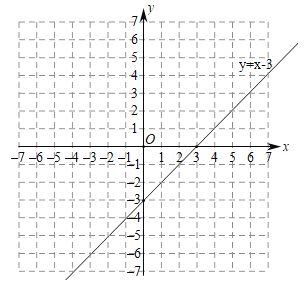
(1)这个函数的表达式为 ;
(2)在给出的平面直角坐标系中,画出这个函数的图象并写出这个函数的--条性质: ;
(3)进一步探究函数图象并解决问题:
①直线![]() 与函数
与函数![]() 有三个交点,则
有三个交点,则![]() ;
;
②已知函数![]() 的图象如图所示,结合你所画的函数图象,写出不等式
的图象如图所示,结合你所画的函数图象,写出不等式![]()
![]() 的解集: .
的解集: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD 中,点E,O,F分别是边AB,AC,AD的中点,连接CE、CF、OE、OF.
(1)求证:△BCE≌△DCF;
(2)当AB与BC满足什么条件时,四边形AEOF正方形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
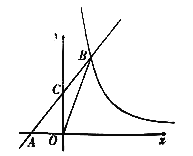
【题目】如图,在平面直角坐标系xOy中,直线y=kx+b(k≠0)与轴交于点A(-2.0),与反比例函数y=![]() (m≠0)的图象交于点B(2,n),连接BO,若S△AOB=4.
(m≠0)的图象交于点B(2,n),连接BO,若S△AOB=4.
(1)求反比例函数和一次函数的表达式:
(2)若直线AB与y轴的交点为C.求△OCB的面积
(3)根据图象,直接写出当x>0时,不等式![]() >kx+b的解集.
>kx+b的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垃圾的分类处理与回收利用,可以减少污染,节省资源.某城市环保部门为了提高宣传实效,抽样调查了部分居民小区一段时间内生活垃圾的分类情况,其相关信息如下:

根据图表解答下列问题:
(1)请将条形统计图补充完整;
(2)在扇形统计图样中,产生的有害垃圾C所对应的圆心角 度;
(3)调查发现,在可回收物中塑料类垃圾占13%,每回收1吨塑料类垃圾可获得0.5吨二级原料.假设该城市每月产生的生活垃圾为1000吨,且全部分类处理,那么每月回收的塑料类垃圾可以获得多少吨二级原料?
查看答案和解析>>
科目:初中数学 来源: 题型:
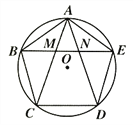
【题目】如图,正五边形的边长为2,连接对角线AD、BE、CE,线段AD分别与BE和CE相交于点M、N,给出下列结论:①∠AME=108°,②AN2=AMAD;③MN=3-![]() ;④S△EBC=2
;④S△EBC=2![]() -1,其中正确的结论是_________(把你认为正确结论的序号都填上).
-1,其中正确的结论是_________(把你认为正确结论的序号都填上).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com