
 如图,已知在△ABC中,∠A=90°.
如图,已知在△ABC中,∠A=90°.分析 (1)作∠ABC的平分线,与AC的交点就是圆心P,此时⊙P与AB,BC两边都相切;
如图,作BC的垂线PD,证明PD和半径相等即可,根据角平分线的性质可得:PA=PD.
(2)要想求劣弧$\widehat{AD}$的长,根据弧长公式需求圆心角∠APD的半径AP的长,利用四边形的内角和求∠APD=135°,再利用勾股定理和等腰三角形的性质求出AP=PD=DC=$\sqrt{2}$-1,代入公式可求弧长.
解答 解: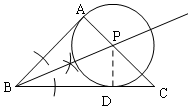 (1)作法:作∠ABC的角平分线交AC于点P,以点P为圆心,AP为半径作圆.
(1)作法:作∠ABC的角平分线交AC于点P,以点P为圆心,AP为半径作圆.
证明:过P作PD⊥BC于D,
∵∠BAC=90°,
∴⊙P与AB相切,
∵BP平分∠ABC,
∴AP=PD,
∵⊙P的半径是PA,
∴PD也是⊙P的半径,即⊙P与BC也相切;
(2)如图,∵⊙P与AB,BC两边都相切,
∴∠BAP=∠BDP=90°,
∵∠ABC=45°,
∴∠APD=360°-90°-90°-45°=135°,
∴∠DPC=45°,
∴△DPC是等腰直角三角形,
∴DP=DC,
在Rt△ABC中,AB=AC=1,
∴CB=$\sqrt{2}$,
∵BP=BP,AP=PD,
∴Rt△ABP≌Rt△DBP,
∴BD=AB=1,
∴CD=PD=AP=$\sqrt{2}$-1,
∴劣弧$\widehat{AD}$的长=$\frac{135π×(\sqrt{2}-1)}{180}$=$\frac{3\sqrt{2}-3}{4}$π.
点评 本题考查了切线的判定、圆的作图以及弧长的计算,首先掌握切线的判定方法:①无交点,作垂线段,证半径;②有交点,作半径,证垂直;本题利用了第①种判定方法;并熟练掌握弧长计算公式:l=$\frac{nπR}{180}$(弧长为l,圆心角度数为n,圆的半径为R).


科目:初中数学 来源: 题型:选择题
| A. | 若x=y,则x-a=y+a | B. | 若$\frac{a}{c}$=$\frac{b}{c}$,则$\frac{a}{{c}^{2}}$=$\frac{b}{{c}^{2}}$ | ||
| C. | 若ac2=bc2,则a=b | D. | 若x=y,则$\frac{x}{a+2}$=$\frac{y}{a+2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在正方形ABCD外侧作直线DE,点C关于直线DE的对称点为M,连接CM,AM.其中AM交直线DE于点N.若45°<∠CDE<90°,则当MN=4,AN=3时,正方形ABCD的边长为( )
如图,在正方形ABCD外侧作直线DE,点C关于直线DE的对称点为M,连接CM,AM.其中AM交直线DE于点N.若45°<∠CDE<90°,则当MN=4,AN=3时,正方形ABCD的边长为( )| A. | $\sqrt{7}$ | B. | 5 | C. | 5$\sqrt{2}$ | D. | $\frac{5}{2}$$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 74 | B. | -74 | C. | 86 | D. | -86 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
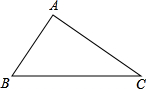 如图,已知在△ABC中,∠A=90°.
如图,已知在△ABC中,∠A=90°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2-5$\sqrt{x}$+4=0是一元二次方程 | |
| B. | ax2+bx+c=0是一元二次方程 | |
| C. | 一元二次方程ax2+bx+c=0(a≠0)的二次项是a | |
| D. | 一元二次方程ax2+bx+c=0(a≠0)的常数项是c |
查看答案和解析>>
科目:初中数学 来源:2016-2017学年四川省眉山市第九年级下学期第一次月考数学试卷(解析版) 题型:单选题
若关于 的一元二次方程的两个根为
的一元二次方程的两个根为 ,
,  ,则这个方程是( )
,则这个方程是( )
A. 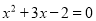 B.
B. 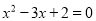
C.  D.
D. 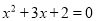
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com