
����Ŀ����ͼ���߳�Ϊ1��������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O����ֱ�ǡ�MPN��ʹֱ�Ƕ���P���O�غϣ�ֱ�DZ�PM��PN�ֱ���OA��OB�غϣ�Ȼ����ʱ����ת��MPN����ת��Ϊ�ȣ�0�㣼�ȣ�90�㣩��PM��PN�ֱ�AB��BC��E��F���㣬����EF��OB�ڵ�G�������н�������ȷ���� ��
��1��EF=![]() OE����2��S�ı���OEBF��S������ABCD=1��4����3��BE+BF=
OE����2��S�ı���OEBF��S������ABCD=1��4����3��BE+BF=![]() OA����4������ת�����У�����BEF���COF�����֮�����ʱ��AE=
OA����4������ת�����У�����BEF���COF�����֮�����ʱ��AE=![]() ����5��OGBD=AE2+CF2��
����5��OGBD=AE2+CF2��
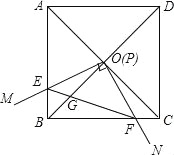
���𰸡���1������2������3������5����
��������
�����������1�����ı���ABCD�������Σ�
��OB=OC����OBE=��OCF=45�㣬��BOC=90�㣬
���BOF+��COF=90�㣬
�ߡ�EOF=90�㣬
���BOF+��COE=90�㣬
���BOE=��COF��
�ڡ�BOE�͡�COF�У�
 ��
��
���BOE�ա�COF��ASA����
��OE=OF��BE=CF��
��EF=![]() OE������ȷ��
OE������ȷ��
��2����S�ı���OEBF=S��BOE+S��BOE=S��BOE+S��COF=S��BOC=![]() S������ABCD��
S������ABCD��
��S�ı���OEBF��S������ABCD=1��4������ȷ��
��3����BE+BF=BF+CF=BC=![]() OA������ȷ��
OA������ȷ��
��4������O��OH��BC��
��BC=1��
��OH=![]() BC=
BC=![]() ��
��
��AE=x����BE=CF=1��x��BF=x��
��S��BEF+S��COF=![]() BEBF+
BEBF+![]() CFOH=
CFOH=![]() x��1��x��+
x��1��x��+![]() ��1��x����
��1��x����![]() =��
=��![]() ��x��
��x��![]() ��2+
��2+![]() ��
��
��a=��![]() ��0��
��0��
�൱x=![]() ʱ��S��BEF+S��COF���
ʱ��S��BEF+S��COF���
������ת�����У�����BEF���COF�����֮�����ʱ��AE=![]() ���ʴ���
���ʴ���
��5���ߡ�EOG=��BOE����OEG=��OBE=45�㣬
���OEG�ס�OBE��
��OE��OB=OG��OE��
��OGOB=OE2��
��OB=![]() BD��OE=
BD��OE=![]() EF��
EF��
��OGBD=EF2��
���ڡ�BEF�У�EF2=BE2+BF2��
��EF2=AE2+CF2��
��OGBD=AE2+CF2������ȷ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
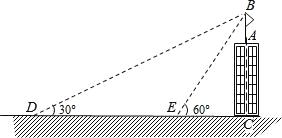
����Ŀ����ͼ��ij������AC������һ���AB���ҵ�A��B��C��ͬһ��ֱ���ϣ�С���ڵ���D���۲���˶���B������Ϊ30�㣬Ȼ�������Խ�����ķ���ǰ����20��������E�����ֲ����˶���B������Ϊ60�㣬��֪������ĸ߶�AC=12m�������AB�ĸ߶ȣ������ȷ��0.1�ף����ο����ݣ���1.73����1.41��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ�� AB=AC��AD=AE����BAC=��DAE����1=25�㣬��2=30�㣬����3=_____.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ԥ��չ���Ż����ȫ��42��ѧ����չ������ϲ�������š��ʾ����飨ÿ��ֻѡһ�����������Ƴ�����ͳ�Ʊ�����ѧ����ϲ������Ŀ�ǣ�������
�������� | ���� | ���� | ���� | ���� |
�������ˣ� | 11 | x | 9 | 8 |
A. ����B. ����C. ����D. ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ں���y=4-3x�У�y��x�������__________���˺���ͼ��________���ޣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
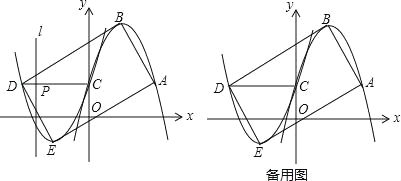
����Ŀ����ͼ1����֪�������µ�������y1=ax2��2ax+1����A��m��1������y�ύ�ڵ�C������ΪB����������y1�Ƶ�C��ת180���õ�������y2����A��B�Ķ�Ӧ��ֱ�Ϊ��D��E��
��1��ֱ��д����A��C��D�����ꣻ
��2�����ı���ABCD�Ǿ���ʱ����a��ֵ��������y2�Ľ���ʽ��
��3���ڣ�2���������£�����DC���߶�DC�ϵĶ���P�ӵ�D��������ÿ��1����λ���ȵ��ٶ��˶�����Cֹͣ���ڵ�P�˶��Ĺ����У�����P��ֱ��l��x�ᣬ������ABDE��ֱ��l�۵���������۵�����غϲ������ΪSƽ����λ����P���˶�ʱ��Ϊt�룬��S��t�ĺ�����ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ�����ݣ�x1��x2��x3������x10����ȥ��һ�����ֵ��һ����Сֵ��������ͳ����һ�����ᷢ���仯���ǣ�������
A.ƽ����B.��λ��C.����D.����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪A��B�Ƿ���������y=![]() ��k��0��x��0��ͼ���ϵ����㣬BC��x�ᣬ��y���ڵ�C������P������ԭ��O��������O��A��B��C��ͼ����������ʾ·�ߣ������˶����յ�ΪC����P��PM��x�ᣬ����ΪM����������OMP�����ΪS��P���˶�ʱ��Ϊt����S����x�ĺ���ͼ�����Ϊ�� ��
��k��0��x��0��ͼ���ϵ����㣬BC��x�ᣬ��y���ڵ�C������P������ԭ��O��������O��A��B��C��ͼ����������ʾ·�ߣ������˶����յ�ΪC����P��PM��x�ᣬ����ΪM����������OMP�����ΪS��P���˶�ʱ��Ϊt����S����x�ĺ���ͼ�����Ϊ�� ��
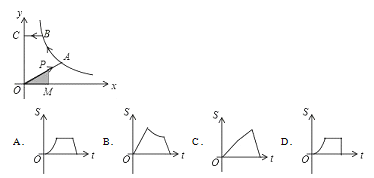
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com