
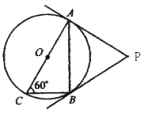
【题目】如图,AC是⊙0的直径,∠ACB=60°,连接AB,过A,B两点分别作⊙O的切线,两切线交于点P.若已知⊙0半径为1,则△PAB的周长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 3
D. 3
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知:∠MON=80°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O 重合),连接AC交射线OE于点D.设∠OAC=x°.
(1)如图1,若AB∥ON,则∠ABO的度数是;
(2)如图2,当∠BAD=∠ABD时,试求x的值(要说明理由);
(3)如图3,若AB⊥OM,则是否存在这样的x的值,使得△ADB中有两个相等的角?若存在,直接写出x的值;若不存在,说明理由.(自己画图) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,最适合采用全面调查的是( )
A. 调查一批汽车的使用寿命 B. 调查春节联欢晚会的收视率
C. 调查某航班的旅客是否携带违禁物品 D. 调查全国七年级学生的视力情况
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=BC=4cm,M是AB的中点,点P、Q分别从A、C两点同时出发,以1cm/s的速度沿AC、CB方向均速运动,到点C、B时停止运动,设运动时间为![]() ,△PMQ的面积为S (cm2),则S (cm2)与
,△PMQ的面积为S (cm2),则S (cm2)与![]() 的函数关系可用图象表示为( )
的函数关系可用图象表示为( )
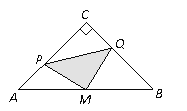
A. 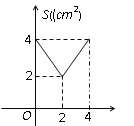 B.
B. 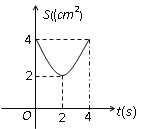 C.
C. 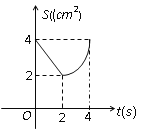 D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com