
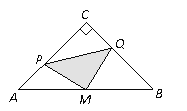
【题目】如图,在△ABC中,∠C=90°,AC=BC=4cm,M是AB的中点,点P、Q分别从A、C两点同时出发,以1cm/s的速度沿AC、CB方向均速运动,到点C、B时停止运动,设运动时间为![]() ,△PMQ的面积为S (cm2),则S (cm2)与
,△PMQ的面积为S (cm2),则S (cm2)与![]() 的函数关系可用图象表示为( )
的函数关系可用图象表示为( )
A. 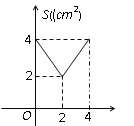 B.
B. 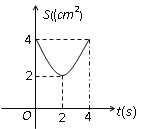 C.
C. 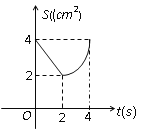 D.
D. 
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
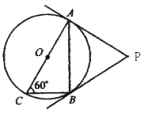
【题目】如图,AC是⊙0的直径,∠ACB=60°,连接AB,过A,B两点分别作⊙O的切线,两切线交于点P.若已知⊙0半径为1,则△PAB的周长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 3
D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】看图填空:已知如图,AD⊥BC于D,EG⊥BC于G,∠E=∠3,求证:AD平分∠BAC. 证明:∵AD⊥BC于D,EG⊥BC于G( 已知 )
∴∠ADC=90°,∠EGC=90°
∴∠ADC=∠EGC(等量代换)
∴AD∥EG
∴∠1=∠3
∠2=∠E
又∵∠E=∠3( 已知)
∴∠1=∠2
∴AD平分∠BAC . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,不正确的是( )
A.三个角的度数之比为1:3:4的三角形是直角三角形
B.三个角的度数之比为3:4:5的三角形是直角三角形
C.三边长度之比为3:4:5的三角形是直角三角形
D.三边长度之比为9:40:41的三角形是直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长不等的正方形依次排列,第一个正方形的边长为1,第二个正方形的边长是第一个正方形边长的2倍,第三个正方形的边长是第二个正方形边长的2倍,依此类推,…….若阴影三角形的面积从左向右依次记为S1、S2、S3、……、Sn,则S4的值为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某港口位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行?为什么? 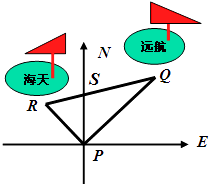
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】荔枝是岭南一带的特色时令水果.今年5月份荔枝一上市,某水果店的老板用3000元购进了一批荔枝,由于荔枝刚在果园采摘比较新鲜,前两天他以高于进价40% 的价格共卖出150千克,由于荔枝保鲜期短,第三天他发现店里的荔枝卖相已不大好,于是果断地将剩余荔枝以低于进价20%的价格全部售出,前后一共获利750元.
(1)若购进的荔枝为![]() 千克,则这批荔枝的进货价为 ;(用含
千克,则这批荔枝的进货价为 ;(用含![]() 的式子来表示)
的式子来表示)
(2)求该水果店的老板这次购进荔枝多少千克.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com