
【题目】已知:∠MON=80°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O 重合),连接AC交射线OE于点D.设∠OAC=x°.
(1)如图1,若AB∥ON,则∠ABO的度数是;
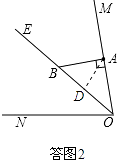
(2)如图2,当∠BAD=∠ABD时,试求x的值(要说明理由);
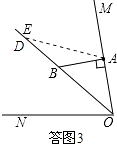
(3)如图3,若AB⊥OM,则是否存在这样的x的值,使得△ADB中有两个相等的角?若存在,直接写出x的值;若不存在,说明理由.(自己画图) 
【答案】
(1)40°
(2)解:②如答图1,∵∠MON=80°,且OE平分∠MON,
∴∠1=∠2=40°,
又∵AB∥ON,
∴∠3=∠1=40°,
∵∠BAD=∠ABD,
∴∠BAD=40°
∴∠4=80°,
∴∠OAC=60°,即x=60°.

(3)存在这样的x,
①如答图2,当点D在线段OB上时,
若∠BAD=∠ABD,则x=40°;
若∠BAD=∠BDA,则x=25°;
若∠ADB=∠ABD,则x=10°.
②如答图3,当点D在射线BE上时,因为∠ABE=130°,且三角形的内角和为180°,
所以只有∠BAD=∠BDA,此时x=130°,C不在ON上,舍去;
综上可知,存在这样的x的值,使得△ADB中有两个相等的角,
且x=10°、25°、40°.
【解析】解:(1)∵∠MON=80°,OE平分∠MON, ∴∠AOB=∠BON=40°,
∵AB∥ON,
∴∠ABO=40°
故答案是:40°;
【考点精析】解答此题的关键在于理解垂线的性质的相关知识,掌握垂线的性质:1、过一点有且只有一条直线与己知直线垂直.2、垂线段最短,以及对平行线的性质的理解,了解两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.


科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋里,装有4个标号为1,2,3,4的小球;它们大小、材质、形状完全相同,甲从布袋中任意摸出一个小球,记下数字为x,乙从剩下的球中任意摸出一个小球,记下数字为y,以此确定点M的坐标(x,y)。
(l)请你用画树状图或列表的方法,写出点M所有可能的坐标;
(2)求点M(x,y)在函数y=![]() 的图象上的概率.
的图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图. 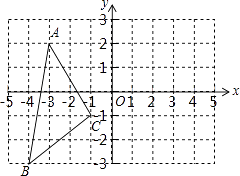
(1)在网格中画出△ABC关于y轴对称的△A1B1C1;
(2)写出△ABC关于x轴对称的△A2B2C2的各顶点坐标;
(3)在y轴上确定一点P,使PA+PB最短.(只需作图保留作图痕迹)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:若m2﹣2mn+2n2﹣8n+16=0,求m、n的值. 解:∵m2﹣2mn+2n2﹣8n+16=0,∴(m2﹣2mn+n2)+(n2﹣8n+16)=0
∴(m﹣n)2+(n﹣4)2=0,∴(m﹣n)2=0,(n﹣4)2=0,∴n=4,m=4.
根据你的观察,探究下面的问题:
(1)a2+b2﹣4a+4=0,则a= . b= .
(2)已知x2+2y2﹣2xy+6y+9=0,求xy的值.
(3)已知△ABC的三边长a、b、c都是正整数,且满足2a2+b2﹣4a﹣6b+11=0,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=∠ACB,以AC为直径的⊙O分别交AB、BC于点M、N,点P在AB的延长线上,且∠CAB=2∠BCP.
(1)求证:直线CP是⊙O的切线.
(2)若BC=2![]() ,sin∠BCP=
,sin∠BCP=![]() ,求点B到AC的距离.
,求点B到AC的距离.
(3)在第(2)的条件下,求△ACP的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
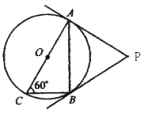
【题目】如图,AC是⊙0的直径,∠ACB=60°,连接AB,过A,B两点分别作⊙O的切线,两切线交于点P.若已知⊙0半径为1,则△PAB的周长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 3
D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)(2﹣π)0+( ![]() )﹣2+(﹣2)3
)﹣2+(﹣2)3
(2)0.5200×(﹣2)202
(3)(﹣2x3)2(﹣x2)÷[(﹣x)2]3
(4)(3x﹣1)(x+1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com