
【题目】计算
(1)(2﹣π)0+( ![]() )﹣2+(﹣2)3
)﹣2+(﹣2)3
(2)0.5200×(﹣2)202
(3)(﹣2x3)2(﹣x2)÷[(﹣x)2]3
(4)(3x﹣1)(x+1)
【答案】
(1)解:原式=1+9﹣8=2;
(2)解:原式=[0.5×(﹣2)]200×(﹣2)2=1×4=4;
(3)解:原式=4x6(﹣x2)÷x6=﹣4x2;
(4)解:原式=3x2+3x﹣x﹣1=3x2+2x﹣1.
【解析】(1)原式利用零指数幂、负整数指数幂法则,以及乘方的意义计算即可得到结果;(2)原式逆用积的乘方及同底数幂的乘法法则计算即可得到结果;(3)原式利用幂的乘方与积的乘方运算法则计算,再利用单项式乘除单项式法则计算即可得到结果;(4)原式利用多项式乘以多项式法则计算即可得到结果.
【考点精析】通过灵活运用零指数幂法则和整数指数幂的运算性质,掌握零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数);aman=am+n(m、n是正整数);(am)n=amn(m、n是正整数);(ab)n=anbn(n是正整数);am/an=am-n(a不等于0,m、n为正整数);(a/b)n=an/bn(n为正整数)即可以解答此题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】下列命题中不正确的是( )
A. 全等三角形的对应边相等 B. 全等三角形的面积相等
C. 全等三角形的周长相等 D. 周长相等的两个三角形全等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:∠MON=80°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O 重合),连接AC交射线OE于点D.设∠OAC=x°.
(1)如图1,若AB∥ON,则∠ABO的度数是;
(2)如图2,当∠BAD=∠ABD时,试求x的值(要说明理由);
(3)如图3,若AB⊥OM,则是否存在这样的x的值,使得△ADB中有两个相等的角?若存在,直接写出x的值;若不存在,说明理由.(自己画图) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,最适合采用全面调查的是( )
A. 调查一批汽车的使用寿命 B. 调查春节联欢晚会的收视率
C. 调查某航班的旅客是否携带违禁物品 D. 调查全国七年级学生的视力情况
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中B(3,2),BC⊥y轴于C,BA⊥x轴于A,点E在线段AB上从B向A以每秒1个单位的速度运动,运动时间为t秒(0<t<2).将BE沿BD折叠,使E点恰好落在BC上的F处.
(1)如图1,若E为AB的中点,请直接写出F、D两点的坐标:F( , ) D( , )
(2)如图1,连接CD,在(1)的条件下,求证:CD=FD.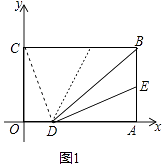
(3)如图2,在E点运动的同时,M点在OC上从C向O运动,N点在OA上从A向O运动,M的运动速度为每秒3个单位,N的运动速度为每秒a个单位.在运动过程中,△CMF能与△ANE全等吗?若能,求出此时a与t的值,若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中, AC=6, BC=4.
(1)用直尺和圆规作∠ACB的角平分线CD,交AB于点D;
(保留作图痕迹,不要求写作法和证明)
(2)在(1)所作的图形中,若△ACD的面积为3,求△BCD的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com