Question

【题目】在平面直角坐标系中B（3，2），BC⊥y轴于C，BA⊥x轴于A，点E在线段AB上从B向A以每秒1个单位的速度运动，运动时间为t秒（0＜t＜2）．将BE沿BD折叠，使E点恰好落在BC上的F处．
（1）如图1，若E为AB的中点，请直接写出F、D两点的坐标：F（ ， ） D（ ， ）
（2）如图1，连接CD，在（1）的条件下，求证：CD=FD．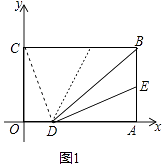

（3）如图2，在E点运动的同时，M点在OC上从C向O运动，N点在OA上从A向O运动，M的运动速度为每秒3个单位，N的运动速度为每秒a个单位．在运动过程中，△CMF能与△ANE全等吗？若能，求出此时a与t的值，若不能，请说明理由．

Answer 1

【答案】
（1）2；2；1；0
（2）

解：如图1，过点D作DG⊥BC于G，

由折叠得，DE=DF，∠BED=∠BFD，

∴∠AED=DFC，

在△AED和△GFD中 ，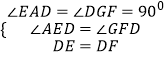

∴△AED≌△GFD，

∴GF=AE=1，

∵CF=2，

∴CG=1，

∴CG=FG，

∵DG⊥CG，

∴CD=FD

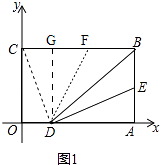
（3）

解：能全等，即：△CMF≌△AEN，

理由：

∵M点在OC上从C向O运动，N点在OA上从A向O运动，M的运动速度为每秒3个单位，N的运动速度为每秒a个单位，点E在线段AB上从B向A以每秒1个单位的速度运动，

∴CM=3t，AN=at，BE=t，

∴AE=2﹣t，

∵将BE沿BD折叠，使E点恰好落在BC上的F处，

∴BF=BE=t，

∴CF=BC﹣BF=3﹣t，

∵BF=BE，BC≠AB，

∴AE=CF，

∵△CMF与△ANE全等

∴△CMF≌△AEN，

∴CM=AE，CF=AN，

∴3t=2﹣t，3﹣t=at，

∴t= ，a=5．

【解析】解：（1）∵四边形ABCD是矩形，且B（3，2），
∴OA=BC=3，OC=AB=2，
∵E为AB的中点，
∴AE=BE=1，
由折叠得，BF=BE=1，
∴CF=2，
∴F（2，2），
如图1，
过点D作DG⊥BC于G，
由折叠得，DE=DF，∠BED=∠BFD，
∴∠AED=DFC，
在△AED和△GFD中 ，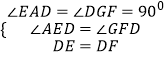
∴△AED≌△GFD，
∴AD=DG=OC=2，
∴OD=1，
∴D（1，0），
所以答案是：2，2，1，0；