
【题目】已知等腰三角形ABC的底边长BC=20cm,D是AC上的一点,且BD=16cm,CD=12cm. 
(1)求证:BD⊥AC;
(2)求△ABC的面积.
【答案】
(1)证明:∵122+162=202,
∴CD2+BD2=BC2,
∴△BDC是直角三角形,
∴BD⊥AC
(2)解:设AD=xcm,则AC=(x+12 )cm,
∵AB=AC,
∴AB═(x+12 )cm,
在Rt△ABD中:AB2=AD2+BD2,
∴(x+12)2=162+x2,
解得x= ![]() ,
,
∴AC= ![]() +12=
+12= ![]() cm,
cm,
∴△ABC的面积S= ![]() BDAC=
BDAC= ![]() ×16×
×16× ![]() =
= ![]() cm2
cm2
【解析】(1)首先根据BD、CD、BC长可利用勾股定理逆定理证明BD⊥AC;(2)设AD=xcm,则AC=(x+12 )cm,在Rt△ABD中,利用勾股定理列出方程求解即可得到AB,进一步得到AC,再利用AC和AC边上的高列式计算即可得解.
【考点精析】根据题目的已知条件,利用等腰三角形的性质和勾股定理的概念的相关知识可以得到问题的答案,需要掌握等腰三角形的两个底角相等(简称:等边对等角);直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=8cm,对角线AC,BD相交于点O,点E,F分别从B,C两点同时出发,以1cm/s的速度沿BC,CD运动,到点C,D时停止运动,设运动时间为t(s),△OEF的面积为s(cm2),则s(cm2)与t(s)的函数关系可用图象表示为( )
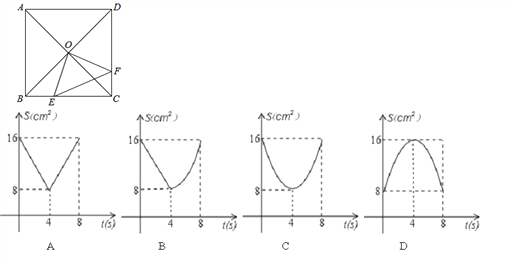
A. (A) B. (B) C. (C) D. (D)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,最适合采用全面调查的是( )
A. 调查一批汽车的使用寿命 B. 调查春节联欢晚会的收视率
C. 调查某航班的旅客是否携带违禁物品 D. 调查全国七年级学生的视力情况
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中B(3,2),BC⊥y轴于C,BA⊥x轴于A,点E在线段AB上从B向A以每秒1个单位的速度运动,运动时间为t秒(0<t<2).将BE沿BD折叠,使E点恰好落在BC上的F处.
(1)如图1,若E为AB的中点,请直接写出F、D两点的坐标:F( , ) D( , )
(2)如图1,连接CD,在(1)的条件下,求证:CD=FD.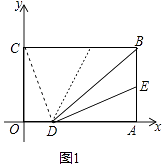
(3)如图2,在E点运动的同时,M点在OC上从C向O运动,N点在OA上从A向O运动,M的运动速度为每秒3个单位,N的运动速度为每秒a个单位.在运动过程中,△CMF能与△ANE全等吗?若能,求出此时a与t的值,若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,点E、F分别为长方形纸带ABCD的边AD、BC上的点,∠DEF=19°,将纸带沿EF折叠成图②(G为ED和EF的交点,再沿BF折叠成图③(H为EF和DG的交点),则图③中∠DHF=° 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com