
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,过点C作CF∥BE交DE的延长线于F.
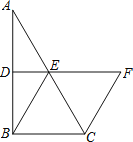
(1)求证:四边形BCFE是菱形;
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
【答案】(1)见解析(1)![]()
【解析】
试题分析:(1)由题意易得,EF与BC平行且相等,故四边形BCFE是平行四边形.又邻边EF=BE,则四边形BCFE是菱形;
(2)连结BF,交CE于点O.利用菱形的性质和等边三角形的判定推知△BCE是等边三角形.通过解直角△BOC求得BO的长度,则BF=2BO.利用菱形的面积=![]() CEBF进行解答.
CEBF进行解答.
(1)证明:∵D、E分别是AB、AC的中点,
∴DE∥BC,BC=2DE.
∵CF∥BE,
∴四边形BCFE是平行四边形.
∵BE=2DE,BC=2DE,
∴BE=BC.
∴□BCFE是菱形;
(2)解:连结BF,交CE于点O.
∵四边形BCFE是菱形,∠BCF=120°,
∴∠BCE=∠FCE=60°,BF⊥CE,
∴△BCE是等边三角形.
∴BC=CE=4.
∴![]() .
.
∴![]() .
.



 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】关于x的方程(m-4)x2+(m+4)x+2m+3=0,当m__________时,是一元二次方程,当m__________时,是一元一次方程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A、0.720精确到百分位 B、5.078×104精确到千分位
C、36万精确到个位 D、2.90×105精确到千位
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PQ为圆O的直径,点B在线段PQ的延长线上,OQ=QB=1,动点A在圆O的上半圆运动(含P、Q两点),以线段AB为边向上作等边三角形ABC.
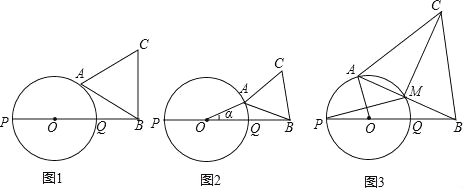
(1)当线段AB所在的直线与圆O相切时,求△ABC的面积(图1);
(2)设∠AOB=α,当线段AB、与圆O只有一个公共点(即A点)时,求α的范围(图2,直接写出答案);
(3)当线段AB与圆O有两个公共点A、M时,如果AO⊥PM于点N,求CM的长度(图3).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列关于直线x=1对称的点是( )
A.点(0,-3)与点(-2,-3)
B.点(2,3)与点(0,3)
C.点(2,3)与点(-2,3)
D.点(2,3)与点(2,-3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,属于假命题的是( )
A. 两点确定一条直线 B. 负数的偶次幂是正数
C. 锐角的补角是钝角 D. 若|﹣x|=﹣x,则x的值为0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,点E,F分别在BC,AC上,且BE=CF,连结AE与BF相交于点G.将△ABC沿AB边折叠得到△ABD,连结DG.延长EA到点H,使得AH=BG,连结DH.
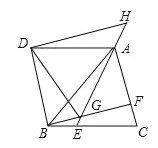
(1)求证:四边形DBCA是菱形.
(2)若菱形DBCA的面积为8![]() ,
,![]() ,求△DGH的面积.
,求△DGH的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com