
【题目】如图,PQ为圆O的直径,点B在线段PQ的延长线上,OQ=QB=1,动点A在圆O的上半圆运动(含P、Q两点),以线段AB为边向上作等边三角形ABC.
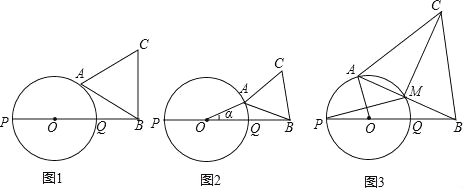
(1)当线段AB所在的直线与圆O相切时,求△ABC的面积(图1);
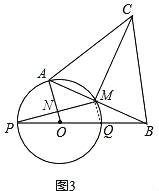
(2)设∠AOB=α,当线段AB、与圆O只有一个公共点(即A点)时,求α的范围(图2,直接写出答案);
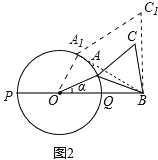
(3)当线段AB与圆O有两个公共点A、M时,如果AO⊥PM于点N,求CM的长度(图3).
【答案】(1)![]() ;(2)0°≤α≤60°;(3)
;(2)0°≤α≤60°;(3)![]() .
.
【解析】
试题分析:(1)连接OA,过点B作BH⊥AC,垂足为H,如图1所示.∵AB与⊙O相切于点A,∴OA⊥AB.∴∠OAB=90°.∵OQ=QB=1,∴OA=1.∴AB=![]() =
=![]() =
=![]() .∵△ABC是等边三角形,∴AC=AB=
.∵△ABC是等边三角形,∴AC=AB=![]() ,∠CAB=60°.∵sin∠HAB=
,∠CAB=60°.∵sin∠HAB=![]() ,∴HB=ABsin∠HAB=
,∴HB=ABsin∠HAB=![]() ×
×![]() =
=![]() .∴S△ABC=
.∴S△ABC=![]() ACBH=
ACBH=![]() ×
×![]() ×
×![]() =
=![]() .∴△ABC的面积为
.∴△ABC的面积为![]() .
.
(2)①当点A与点Q重合时,线段AB与圆O只有一个公共点,此时α=0°;
②当线段A1B所在的直线与圆O相切时,如图2所示,线段A1B与圆O只有一个公共点,此时OA1⊥BA1,OA1=1,OB=2,∴cos∠A1OB=![]() =
=![]() .∴∠A1OB=60°.∴当线段AB与圆O只有一个公共点(即A点)时,α的范围为:0°≤α≤60°.
.∴∠A1OB=60°.∴当线段AB与圆O只有一个公共点(即A点)时,α的范围为:0°≤α≤60°.
(3)连接MQ,如图3所示.∵PQ是⊙O的直径,∴∠PMQ=90°.∵OA⊥PM,∴∠PNO=90°.
∴∠PNO=∠PMQ.∴ON∥MQ.∴△PNO∽△PMQ.∴![]() =
=![]() =
=![]() ,∵PO=OQ=
,∵PO=OQ=![]() PQ.∴PN=
PQ.∴PN=![]() PM,ON=
PM,ON=![]() MQ.同理:MQ=
MQ.同理:MQ=![]() AO,BM=
AO,BM=![]() AB.∵AO=1,∴MQ=
AB.∵AO=1,∴MQ=![]() .∴ON=
.∴ON=![]() .∵∠PNO=90°,PO=1,ON=
.∵∠PNO=90°,PO=1,ON=![]() ,∴PN=
,∴PN=![]() .∴PM=
.∴PM=![]() .∴NM=
.∴NM=![]() .∵∠ANM=90°,AN=A0﹣ON=
.∵∠ANM=90°,AN=A0﹣ON=![]() ,∴AM=
,∴AM=![]() =
=![]() =
=![]() .∵△ABC是等边三角形,∴AC=AB=BC,∠CAB=60°.∵BM=
.∵△ABC是等边三角形,∴AC=AB=BC,∠CAB=60°.∵BM=![]() AB,∴AM=BM.∴CM⊥AB.∵AM=
AB,∴AM=BM.∴CM⊥AB.∵AM=![]() ,∴BM=
,∴BM=![]() ,AB=
,AB=![]() .∴AC=
.∴AC=![]() .∴CM=
.∴CM=![]() =
=![]() =
=![]() .∴CM的长度为
.∴CM的长度为![]() .
.


科目:初中数学 来源: 题型:
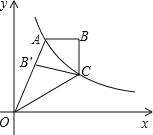
【题目】如图,双曲线y=![]() (x>0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴正半轴的夹角,AB∥x轴.将△ABC沿AC翻折后得△AB′C,B′点落在OA上,则四边形OABC的面积是 .
(x>0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴正半轴的夹角,AB∥x轴.将△ABC沿AC翻折后得△AB′C,B′点落在OA上,则四边形OABC的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序为(1,0)、(2,0)、(2,1)、(1,1)、(1,2)、(2,2)…根据这个规律,第2016个点的坐标为( )
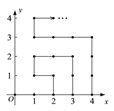
A(45,9) B(45,13) C(45,22) D(45,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,过点C作CF∥BE交DE的延长线于F.
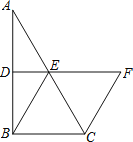
(1)求证:四边形BCFE是菱形;
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】麒麟区是云南省曲靖市政府所在地,位于云南省东部,滇东高原中部,南盘江上游,截止2018年末麒麟区有常住人口约76万人,76万这个数字用科学记数法表示为( )
A. 0.76×106B. 7.6×105C. 76×104D. 7.6×106
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个三角形能被一条线段分割成两个等腰三角形,那么称这条线段为这个三角形的特异线,称这个三角形为特异三角形.
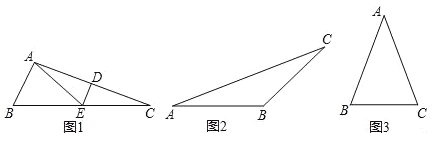
(1)如图1,△ABC中,∠B=2∠C,线段AC的垂直平分线交AC于点D,交BC于点E.求证:AE是△ABC的一条特异线.
(2)如图2,已知△ABC是特异三角形,且∠A=30°,∠B为钝角,求出所有可能的∠B的度数.
(3)如图3,△ABC是一个腰长为2的等腰锐角三角形,且它是特异三角形,若它的顶角度数为整数,请求出其特异线的长度;若它的顶角度数不是整数,请直接写出顶角度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com