
【题目】如果一个三角形能被一条线段分割成两个等腰三角形,那么称这条线段为这个三角形的特异线,称这个三角形为特异三角形.
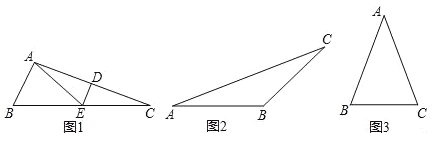
(1)如图1,△ABC中,∠B=2∠C,线段AC的垂直平分线交AC于点D,交BC于点E.求证:AE是△ABC的一条特异线.
(2)如图2,已知△ABC是特异三角形,且∠A=30°,∠B为钝角,求出所有可能的∠B的度数.
(3)如图3,△ABC是一个腰长为2的等腰锐角三角形,且它是特异三角形,若它的顶角度数为整数,请求出其特异线的长度;若它的顶角度数不是整数,请直接写出顶角度数.
【答案】(1)AE是△ABC是一条特异线
(2)符合条件的∠ABC的度数为135°或112.5°或140°.
(3)若它的顶角度数不是整数,则顶角度数为(![]() )°.
)°.
【解析】
试题分析:(1)只要证明△ABE,△AEC是等腰三角形即可.
(2)如图2中,当BD是特异线时,分三种情形讨论,如图3中,当AD是特异线时,AB=BD,AD=DC根据等腰三角形性质即可解决问题,当CD为特异线时,不合题意.
(3)如图3中,当BD是特异线时,分两种情形讨论即可.当AD是特异线时,不合题意.
试题解析:(1)证明:如图1中,
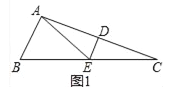
∵DE是线段AC的垂直平分线,
∴EA=EC,即△EAC是等腰三角形,
∴∠EAC=∠C,
∴∠AEB=∠EAC+∠C=2∠C,
∵∠B=2∠C,
∴∠AEB=∠B,即△EAB是等腰三角形,
∴AE是△ABC是一条特异线.
(2)如图2中,
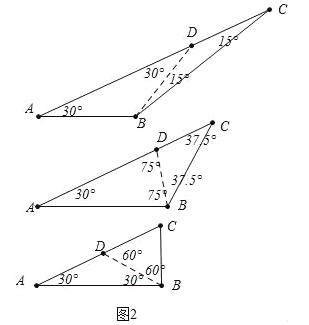
当BD是特异线时,如果AB=BD=DC,则∠ABC=∠ABD+∠DBC=120°=15°=135°,
如果AD=AC,DB=DC,则∠ABC=∠ABD+∠DBC=75°+37.5°=112.5°,
如果AD=DB,DC=DB,则ABC=∠ABD+∠DBC=30°+60°=90°(不合题意舍弃).
如图3中,当AD是特异线时,AB=BD,AD=DC,则∠ABC=180°﹣20°﹣20°=140°
当CD为特异线时,不合题意.
∴符合条件的∠ABC的度数为135°或112.5°或140°.
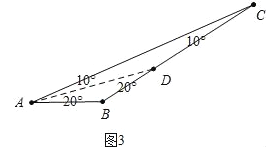
(3)如图3中,
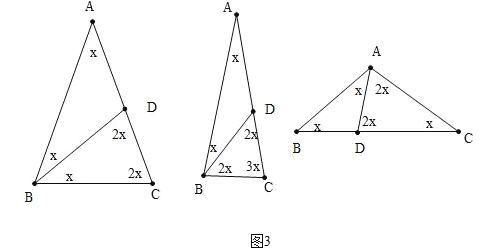
当BD是特异线时,有两种情形,如果AD=BD=BC,设∠A=x,则x+2x+2x=180°,解得x=36°,
设AD=BD=BC=a,
由△BCD∽△ABC得到![]() ,
,
∴![]() ,
,
∴a2+2a﹣4=0,
∴a=﹣1+![]() 或﹣1﹣
或﹣1﹣![]() (舍弃).
(舍弃).
如果AD=BC,BC=CD,设∠A=x,则2x+2x+3x=180°解得x=(![]() )°.
)°.
当AD是特异线时,如果DA=DB,CA=CD,设∠B=∠C=x,则x+2x+2x=180°,解得x=36°,
∴∠BAC=108°,不符合题意.
∴△ABC是一个腰长为2的等腰锐角三角形,且它是特异三角形,若它的顶角度数为整数,其特异线的长度为﹣1+![]() ,
,
若它的顶角度数不是整数,则顶角度数为(![]() )°.
)°.


科目:初中数学 来源: 题型:
【题目】如图,PQ为圆O的直径,点B在线段PQ的延长线上,OQ=QB=1,动点A在圆O的上半圆运动(含P、Q两点),以线段AB为边向上作等边三角形ABC.
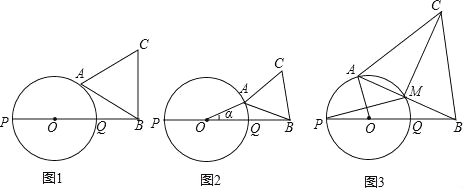
(1)当线段AB所在的直线与圆O相切时,求△ABC的面积(图1);
(2)设∠AOB=α,当线段AB、与圆O只有一个公共点(即A点)时,求α的范围(图2,直接写出答案);
(3)当线段AB与圆O有两个公共点A、M时,如果AO⊥PM于点N,求CM的长度(图3).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年6月,全国参加高等院校统一招生考试的学生约10 200 000人,其中10 200 000用科学记数法表示应为( )
A. 10.2×106 B. 1.02×107 C. 0.102×108 D. 1.02×109
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,点E,F分别在BC,AC上,且BE=CF,连结AE与BF相交于点G.将△ABC沿AB边折叠得到△ABD,连结DG.延长EA到点H,使得AH=BG,连结DH.
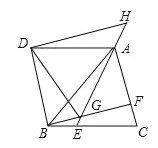
(1)求证:四边形DBCA是菱形.
(2)若菱形DBCA的面积为8![]() ,
,![]() ,求△DGH的面积.
,求△DGH的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列四个命题:①直径所对的圆周角是直角;②圆既是轴对称图形,又是中心对称图形;③在同圆中,相等的圆周角所对的弦相等;④三点确定一个圆.其中正确命题的个数为( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列四个命题:①对顶角相等;②内错角相等;③平行于同一条直线的两条直线互相平行; ④如果一个角的两边分别平行于另一个角的两边,那么这两个角相等.其中真命题的是__________(填序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com