
【题目】在平面直角坐标系xOy中,抛物线y=ax2-2ax-3a(a≠0)顶点为P,且该抛物线与x轴交于A,B两点(点A在点B的左侧).我们规定:抛物线与x轴围成的封闭区域称为“G区域”(不包含边界);横、纵坐标都是整数的点称为整点.
(1)求抛物线y=ax2-2ax-3a顶点P的坐标(用含a的代数式表示);
(2)如果抛物线y=ax2-3ax-3a经过(1,3).
①求a的值;
②在①的条件下,直接写出“G区域”内整点的个数.
(3)如果抛物线y=ax2-2ax-3a在“G区域”内有4个整点,直接写出a的取值范围.
【答案】(1)顶点P的坐标为(1,-4a).(2)①a=-![]() .②“G区域”有6个整数点.(3)a的取值范围为-
.②“G区域”有6个整数点.(3)a的取值范围为-![]() ≤a<-
≤a<-![]() 或
或![]() <a≤
<a≤![]() .
.
【解析】
(1)利用配方法将抛物线的解析式变形为顶点式,由此即可得出顶点P的坐标;
(2)将点(1,3)代入抛物线解析式中,即可求出a值,再分析当x=0、1、2时,在“G区域”内整数点的坐标,由此即可得出结论;
(3)分a<0及a>0两种情况考虑,依照题意画出图形,结合图形找出关于a的不等式组,解之即可得出结论.
解:(1)∵y=ax2-2ax-3a=a(x+1)(x-3)=a(x-1)2-4a,
∴顶点P的坐标为(1,-4a).
(2)∵抛物线y=a(x+1)(x-3)经过(1,3),
∴3=a(1+1)(1-3),
解得:a=-![]() .
.
当y=-![]() (x+1)(x-3)=0时,x1=-1,x2=3,
(x+1)(x-3)=0时,x1=-1,x2=3,
∴点A(-1,0),点B(3,0).
当x=0时,y=-![]() (x+1)(x-3)=
(x+1)(x-3)=![]() ,
,
∴(0,1)、(0,2)两个整数点在“G区域”;
当x=1时,y=-![]() (x+1)(x-3)=3,
(x+1)(x-3)=3,
∴(1,1)、(1,2)两个整数点在“G区域”;
当x=2时,y=-![]() (x+1)(x-3)=
(x+1)(x-3)=![]() ,
,
∴(2,1)、(2,2)两个整数点在“G区域”.
综上所述:此时“G区域”有6个整数点.
(3)当x=0时,y=a(x+1)(x-3)=-3a,
∴抛物线与y轴的交点坐标为(0,-3a).
当a<0时,如图1所示,
此时有![]() ,
,
解得:-![]() ≤a<-
≤a<-![]() ;
;
当a>0时,如图2所示,
此时有![]() ,
,
解得:![]() <a≤
<a≤![]() .
.
综上所述,如果G区域中仅有4个整数点时,则a的取值范围为-![]() ≤a<-
≤a<-![]() 或
或![]() <a≤
<a≤![]() .
.



科目:初中数学 来源: 题型:
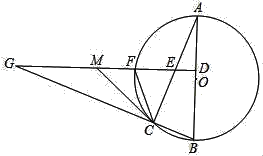
【题目】如图,在⊙O中,AB为直径,AC为弦.过BC延长线上一点G,作GD⊥AO于点D,交AC于点E,交⊙O于点F,M是GE的中点,连接CF,CM.
(1)判断CM与⊙O的位置关系,并说明理由;
(2)若∠ECF=2∠A,CM=6,CF=4,求MF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
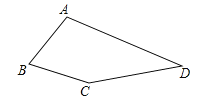
【题目】如图,在四边形ABCD中,∠B=60°,∠D=30°,AB=BC.
(1)求∠A+∠C的度数;
(2)连接BD,探究AD,BD,CD三者之间的数量关系,并说明理由;
(3)若AB=1,点E在四边形ABCD内部运动,且满足AE2=BE2+CE2,求点E运动路径的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
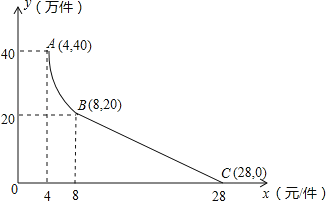
【题目】某公司用100万元研发一种市场急需电子产品,已于当年投入生产并销售,已知生产这种电子产品的成本为4元/件,在销售过程中发现:每年的年销售量y(万件)与销售价格x(元/件)的关系如图所示,其中AB为反比例函数图象的一部分,设公司销售这种电子产品的年利润为s(万元).
(1)请求出y(万件)与x(元/件)的函数表达式;
(2)求出第一年这种电子产品的年利润s(万元)与x(元/件)的函数表达式,并求出第一年年利润的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明同学设计的“已知底边及底边上的高作等腰三角形”的尺规作图的过程.
已知:如图1,线段a和线段b.
求作:△ABC,使得AB=AC,BC=a,BC边上的高为b.
作法:如图2,
①作射线BM,并在射线BM上截取BC=a;
②作线段BC的垂直平分线PQ,PQ交BC于D;
③以D为圆心,b为半径作圆,交PQ于A;
④连接AB和AC.
则△ABC就是所求作的图形.
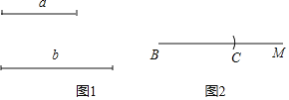
根据上述作图过程,回答问题:
(1)用直尺和圆规,补全图2中的图形;
(2)完成下面的证明:
证明:由作图可知BC=a,AD=b.
∵PQ为线段BC的垂直平分线,点A在PQ上,
∴AB=AC(______)(填依据).
又∵AD在线段BC的垂直平分线PQ上,
∴AD⊥BC.
∴AD为BC边上的高,且AD=b.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:四边形ABCD的对角线AC、BD相交于点O,给出下列4个条件:①AB∥CD;②OA=OC;③AB=CD;④AD∥BC从中任取两个条件,能推出四边形ABCD是平行四边形的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,A,B分别在射线OM,ON上,且∠MON为钝角,现以线段OA,OB为斜边向∠MON的外侧作等腰直角三角形,分别是△OAP,△OBQ,点C,D,E分别是OA,OB,AB的中点.
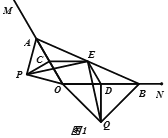
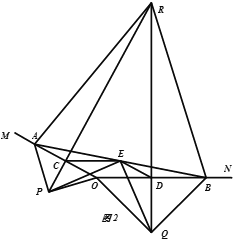
(1)求证:四边形OCED为平行四边形;
(2)求证:△PCE≌△EDQ
(3)如图2,延长PC,QD交于点R.若∠MON=150°,求证:△ABR为等边三角形。
查看答案和解析>>
科目:初中数学 来源: 题型:
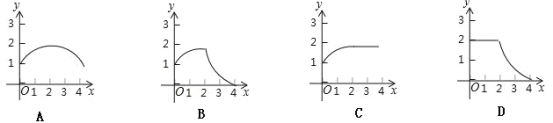
【题目】如图1,△ABC和△DEF都是等腰直角三角形,其中∠C=∠EDF=90°,点A与点D重合,点E在AB上,AB=4,DE=2.如图2,△ABC保持不动,△DEF沿着线段AB从点A向点B移动,当点D与点B重合时停止移动.设AD=x,△DEF与△ABC重叠部分的面积为y,则y关于x的函数图象大致是( )
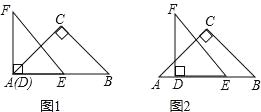
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“春节”假期间,小明和小华都准备在某市的九龙瀑布(记为A)、凤凰谷(记为B)、彩色沙林(记为C)、海峰湿地(记为D)这四个景点中任选一个去游玩,每个景点被选中的可能性相同.
(1)求小明去凤凰谷的概率;
(2)用树状图或列表的方法求小明和小华都去九龙瀑布的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com