
����Ŀ��������С��ͬѧ��Ƶ�����֪�ױ��ױ��ϵĸ����������������ij߹���ͼ�Ĺ��̣�
��֪����ͼ1���߶�a���߶�b��
��������ABC��ʹ��AB=AC��BC=a��BC���ϵĸ�Ϊb��
��������ͼ2��
��������BM����������BM�Ͻ�ȡBC=a��
�����߶�BC�Ĵ�ֱƽ����PQ��PQ��BC��D��
����DΪԲ�ģ�bΪ�뾶��Բ����PQ��A��
������AB��AC��
����ABC������������ͼ�Σ�
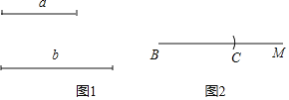
����������ͼ���̣��ش����⣺
��1����ֱ�ߺ�Բ�棬��ȫͼ2�е�ͼ�Σ�
��2����������֤����
֤��������ͼ��֪BC=a��AD=b��
��PQΪ�߶�BC�Ĵ�ֱƽ���ߣ���A��PQ�ϣ�
��AB=AC��______���������ݣ���
�֡�AD���߶�BC�Ĵ�ֱƽ����PQ�ϣ�
��AD��BC��
��ADΪBC���ϵĸߣ���AD=b��
���𰸡���1����ͼ����������2���߶εĴ�ֱƽ�����ϵĵ㵽�߶ε������˵�ľ������
��������
��1������Ҫ�����ó߹����������μ��ɣ�
��2�������߶εĴ�ֱƽ���ߵ����ʶ������ɽ�����⣮
�⣺��1����ABC��Ϊ����
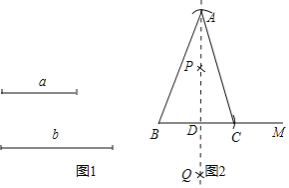
��2������ͼ��֪BC=a��AD=b��
��PQΪ�߶�BC�Ĵ�ֱƽ���ߣ���A��PQ�ϣ�
��AB=AC���߶εĴ�ֱƽ�����ϵĵ㵽�߶ε������˵�ľ�����ȣ��������ݣ���
�֡�AD���߶�BC�Ĵ�ֱƽ����PQ�ϣ�
��AD��BC��
��ADΪBC���ϵĸߣ���AD=b��
�ʴ�Ϊ���߶εĴ�ֱƽ�����ϵĵ㵽�߶ε������˵�ľ�����ȣ�


 ��ѧ��ʦ����ϵ�д�
��ѧ��ʦ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
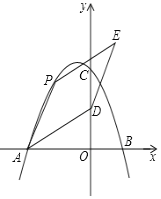
����Ŀ����ͼ����ƽ��ֱ������ϵ�У����κ���y����x2+bx+c��ͼ���������ύ��A��B��C���㣬���е�B������Ϊ��1��0������C������Ϊ��0��4������D������Ϊ��0��2������PΪ���κ���ͼ���ϵĶ��㣮
��1������κ����ı���ʽ��
��2������Pλ�ڵڶ������ڶ��κ�����ͼ����ʱ������AD��AP����AD��APΪ�ڱ���ƽ���ı���APED����ƽ���ı���APED�����ΪS����S�����ֵ��
��3����y�����Ƿ���ڵ�F��ʹ��PDF���ADO���ࣿ�����ڣ�ֱ��д����P�ĺ����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
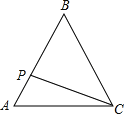
����Ŀ����ͼ������ABC�ı߳�Ϊ3cm,����P�ӵ�A��������ÿ��1cm���ٶȣ���![]() �ķ����˶��������Cʱֹͣ�����˶�ʱ��Ϊx���룩��
�ķ����˶��������Cʱֹͣ�����˶�ʱ��Ϊx���룩��![]() ,��y����x�ĺ�����ͼ�����Ϊ�� ��
,��y����x�ĺ�����ͼ�����Ϊ�� ��
A. 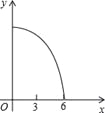 B.
B.  C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC�ǵ���ֱ�������Σ�AB��AC��DΪƽ���ڵ�����һ�㣬������CD��AC������ADB����ADΪ���ĵ��������Σ����CDB�Ķ���Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�ţ�1���չ��ѧ����������Ż���λͬѧ�����ò���Dz���ѧУ��˵ĸ߶ȣ�����վ��B������˶���E�������Ϊ45�㣬�Ż�վ��D��D����ֱ��FB�ϣ������˶���E������Ϊ15�㣬��֪�������Ż���ࣨBD��30�ף����������ߣ�AB��1.6�ף��Ż������ߣ�CD��1.75�ף�����˵ĸ�EF�ij����������ȷ��0.1���ο����ݣ�sin15���0.26��cos15���0.97��tan15���0.27��
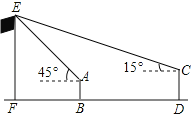
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�������y=ax2-2ax-3a��a��0������ΪP���Ҹ���������x�ύ��A��B���㣨��A�ڵ�B����ࣩ�����ǹ涨����������x��Χ�ɵķ�������Ϊ��G���������������߽磩���ᡢ�����궼�������ĵ��Ϊ���㣮
��1����������y=ax2-2ax-3a����P�����꣨�ú�a�Ĵ���ʽ��ʾ����
��2�����������y=ax2-3ax-3a������1��3����
����a��ֵ��
���ڢٵ������£�ֱ��д����G������������ĸ�����
��3�����������y=ax2-2ax-3a����G����������4�����㣬ֱ��д��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��������ACB��AC=3��BC=4����ֱ�Ƕ���C��CA1��AB������ΪA1���ٹ�A1��A1C1��BC������ΪC1����CA1��C1A2��AB������ΪA2���ٹ�A2��A2C2��BC������ΪC2����������һֱ����ȥ���õ�һ���߶�A1C1��C2A2���������߶�AnCn=___.
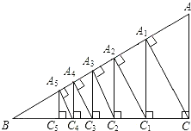
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ı���ABCD�������Σ�����ֱ�ǡ�AEF��ֱ�Ƕ���E��BC�ϣ�(����B��C�غ�)��FM��AD��������AD�ڵ�M��
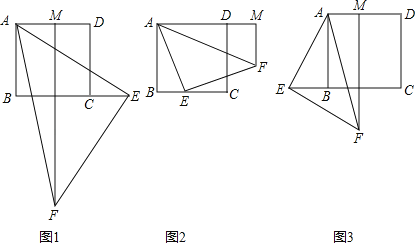
(1)��ͼ1������E�ڱ�BC���ӳ����ϣ���M�ڱ�AD��ʱ����ֱ��д���߶�AB��BE��AM֮���������ϵ������Ҫ֤��.
(2)��ͼ2������E�ڱ�BC�ϣ���M�ڱ�AD���ӳ�����ʱ����д���߶�AB��BE��AM֮���������ϵ������֤����Ľ���.
(3)��ͼ3������E�ڱ�CB���ӳ����ϣ���M�ڱ�AD��ʱ����BE��![]() ����AFM��15������AM�ij���.
����AFM��15������AM�ij���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��չ������ϲ����һ������������飬Ҫ��ÿ��ѧ����ѡ��ֻ��ѡһ�����������m��ѧ���������������Ƴ����²�����������ͼ������ͼ������������Ϣ����������⣺
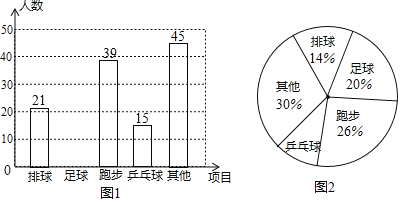
��1����m��ֵ��
��2���벹ȫ���������ͳ��ͼ��
��3����ͼ2�У���ƹ��������Ӧ���ε�Բ�ĽǵĶ���Ϊ���ٶȣ�
��4����֪��У����1200��ѧ����������Ƹ�УԼ�ж�����ѧ����ϲ��������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com