
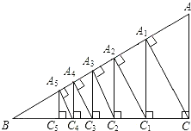
【题目】如图,已知直角三角形ACB,AC=3,BC=4,过直角顶点C作CA1⊥AB,垂足为A1,再过A1作A1C1⊥BC,垂足为C1;过CA1作C1A2⊥AB,垂足为A2,再过A2作A2C2⊥BC,垂足为C2;…,这样一直做下去,得到一组线段A1C1,C2A2,…,则线段AnCn=___.
科目:初中数学 来源: 题型:
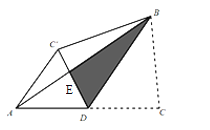
【题目】如图,在△ABC中,D是AC边上的中点,连结BD,把△BDC′沿BD翻折,得到△![]() ,DC与AB交于点E,连结
,DC与AB交于点E,连结![]() ,若AD=AC′=2,BD=3则点D到BC的距离为( )
,若AD=AC′=2,BD=3则点D到BC的距离为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,BC的延长线于⊙O的切线AF交于点F.
(1)求证:∠ABC=2∠CAF;
(2)若AC=2![]() ,CE:EB=1:4,求CE的长.
,CE:EB=1:4,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明同学设计的“已知底边及底边上的高作等腰三角形”的尺规作图的过程.
已知:如图1,线段a和线段b.
求作:△ABC,使得AB=AC,BC=a,BC边上的高为b.
作法:如图2,
①作射线BM,并在射线BM上截取BC=a;
②作线段BC的垂直平分线PQ,PQ交BC于D;
③以D为圆心,b为半径作圆,交PQ于A;
④连接AB和AC.
则△ABC就是所求作的图形.
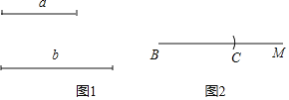
根据上述作图过程,回答问题:
(1)用直尺和圆规,补全图2中的图形;
(2)完成下面的证明:
证明:由作图可知BC=a,AD=b.
∵PQ为线段BC的垂直平分线,点A在PQ上,
∴AB=AC(______)(填依据).
又∵AD在线段BC的垂直平分线PQ上,
∴AD⊥BC.
∴AD为BC边上的高,且AD=b.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的动点P和图形N,给出如下定义:如果Q为图形N上一个动点,P,Q两点间距离的最大值为dmax,P,Q两点间距离的最小值为dmin,我们把dmax+dmin的值叫点P和图形N间的“和距离”,记作d(P,图形N).
(1)如图1,正方形ABCD的中心为点O,A(3,3).
①点O到线段AB的“和距离”d(O,线段AB)=______;
②设该正方形与y轴交于点E和F,点P在线段EF上,d(P,正方形ABCD)=7,求点P的坐标.
(2)如图2,在(1)的条件下,过C,D两点作射线CD,连接AC,点M是射线CD上的一个动点,如果6![]() <d(M,线段AC)<6+3
<d(M,线段AC)<6+3![]() ,直接写出M点横坐标t取值范围.
,直接写出M点横坐标t取值范围.
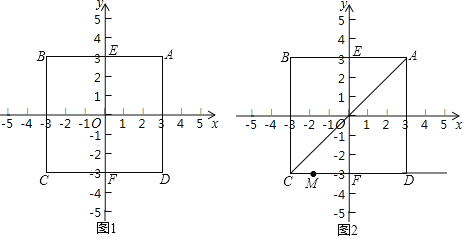
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,A,B分别在射线OM,ON上,且∠MON为钝角,现以线段OA,OB为斜边向∠MON的外侧作等腰直角三角形,分别是△OAP,△OBQ,点C,D,E分别是OA,OB,AB的中点.
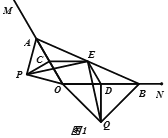
(1)求证:四边形OCED为平行四边形;
(2)求证:△PCE≌△EDQ
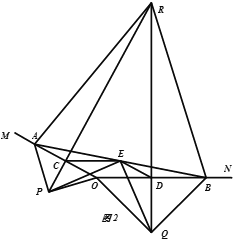
(3)如图2,延长PC,QD交于点R.若∠MON=150°,求证:△ABR为等边三角形。
查看答案和解析>>
科目:初中数学 来源: 题型:
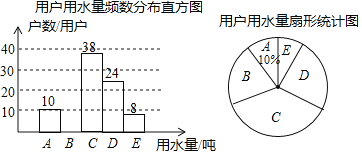
【题目】我市为了节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费为更好地决策,自来水公司在某街道随机抽取了部分用户的用水量数据,按A,B,C,D,E五个区间进行统计,并将统计结果绘制如下两幅不完整的统计图,请你结合图中所给信息解答下列问题:(说明:A:0﹣3吨;B:3﹣6吨;C:6﹣9吨;D:9﹣12吨;E:12﹣16吨,且每组数据区间包括右端的数但不包括左端的数)
(1)这次随机抽样调查了_____用户
(2)补全频数分布直方图,求扇形统计图中B部分的圆心角的度数;
(3)如果自来水公司将基本用水量定为每户9吨,那么该街道1.8万用户中约有多少用户的用水全部享受基本用水量的价格?
查看答案和解析>>
科目:初中数学 来源: 题型:
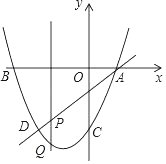
【题目】如图,抛物线y=x2+bx﹣3过点A(1,0),直线AD交抛物线于点D,点D的横坐标为﹣2,点P是线段AD上的动点.
(1)b= ,抛物线的顶点坐标为 ;
(2)求直线AD的解析式;
(3)过点P的直线垂直于x轴,交抛物线于点Q,连接AQ,DQ,当△ADQ的面积等于△ABD的面积的一半时,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
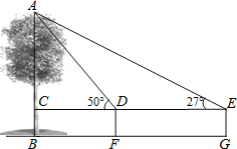
【题目】某数学兴趣小组用高为1.2米的测角仪测量小树AB的高度,如图,在距AB一定距离的F处测得小树顶部A的仰角为50°,沿BF方向行走3.5米到G处时,又测得小树顶部A的仰角为27°,求小树AB的高度.(参考数据:sin27°=0.45,cos27°=0.89,tan27°=0.5,sin50°=0.77,cos50°=0.64,tan50°=1.2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com