练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

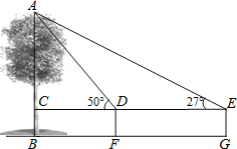
    【题目】某数学兴趣小组用高为1.2米的测角仪测量小树AB的高度，如图，在距AB一定距离的F处测得小树顶部A的仰角为50°，沿BF方向行走3.5米到G处时，又测得小树顶部A的仰角为27°，求小树AB的高度．（参考数据：sin27°=0.45，cos27°=0.89，tan27°=0.5，sin50°=0.77，cos50°=0.64，tan50°=1.2）

    【答案】4.2米

    【解析】

    首先设AC=x米，然后由在Rt△ACD中，tan50= ,求得CD，由在Rt△ACE中，tan27°= ，求得CE，又由CE-CD=DE，即可得方程，继而求得答案

    解：设AC＝x米，

    在Rt△ACD中，tan50°＝，

    ∴CD＝＝ ＝ x，

    在Rt△ACE中，tan27°＝，

    ∴CE＝＝＝2x，

    ∵CE﹣CD＝DE，

    ∴2x﹣x＝3.5．

    解得x＝3．

    ∴AB＝AC+CB＝3+1.2＝4.2（米）．

    答：小树AB的高为4.2米．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

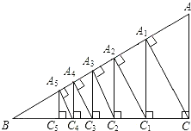
    【题目】如图，已知直角三角形ACB，AC=3，BC=4，过直角顶点C作CA1⊥AB，垂足为A1，再过A1作A1C1⊥BC，垂足为C1；过CA1作C1A2⊥AB，垂足为A2，再过A2作A2C2⊥BC，垂足为C2；…，这样一直做下去，得到一组线段A1C1，C2A2，…，则线段AnCn=___.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

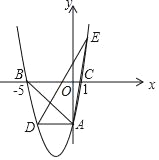
    【题目】如图，在平面直角坐标系中，抛物线y=ax2+bx﹣5交y轴于点A，交x轴于点B（﹣5，0）和点C（1，0），过点A作AD∥x轴交抛物线于点D．

    （1）求此抛物线的表达式；

    （2）点E是抛物线上一点，且点E关于x轴的对称点在直线AD上，求△EAD的面积；

    （3）若点P是直线AB下方的抛物线上一动点，当点P运动到某一位置时，△ABP的面积最大，求出此时点P的坐标和△ABP的最大面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校开展“我最喜爱的一项体育活动”调查，要求每名学生必选且只能选一项，现随机抽查了m名学生，并将其结果绘制成如下不完整的条形图和扇形图，请结合以上信息解答下列问题：

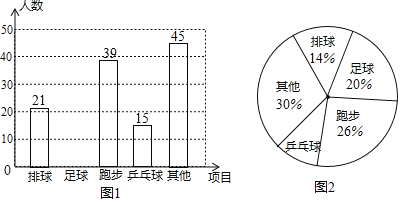
    （1）求m的值；

    （2）请补全上面的条形统计图；

    （3）在图2中，“乒乓球”所对应扇形的圆心角的度数为多少度？

    （4）已知该校共有1200名学生，请你估计该校约有多少名学生最喜爱足球活动？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线（a≠0）的对称轴为直线x＝1，与x轴的交点（，0），（，0），且﹣1＜＜0＜，有下列5个结论：①abc＜0；②b＞a+c；③a+b＞k（ka+b）（k为常数，且k≠1）；④2c＜3b；⑤若抛物线顶点坐标为（1，n），则＝4a（c﹣n），其中正确的结论有（　　）个．

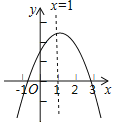
    A. 5B. 4C. 3D. 2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某水产养殖大户为了更好地发挥技术优势，一次性收购了20000kg淡水鱼，计划养殖一段时间后再出售．已知每天放养的费用相同，放养10天的总成本为30.4万元；放养20天的总成本为30.8万元（总成本=放养总费用+收购成本）．

    （1）设每天的放养费用是a万元，收购成本为b万元，求a和b的值；

    （2）设这批淡水鱼放养t天后的质量为m（kg），销售单价为y元/kg．根据以往经验可知：m与t的函数关系为；y与t的函数关系如图所示．

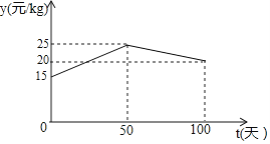
    ①分别求出当0≤t≤50和50＜t≤100时，y与t的函数关系式；

    ②设将这批淡水鱼放养t天后一次性出售所得利润为W元，求当t为何值时，W最大？并求出最大值．（利润=销售总额-总成本）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】己知抛物线y=ax2+bx－3a(a>0)与x轴交于A(－1,0)、B两点，与y轴交于点C.

    (1)求点B的坐标；

    (2)P是第四象限内抛物线上的一个动点.

    ①若∠APB=90°，且a<3，求点P纵坐标的取值范围；

    ②直线PA、PB分别交y轴于点M、N求证：为定值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

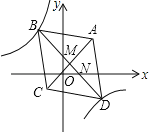
    【题目】如图，在平面直角坐标系xOy中，菱形ABCD的顶点A（4，4），C（﹣2，﹣2），点B，D在反比例函数的图象上，对角线BD交AC于点M，交x轴于点N，若，则k的值是_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

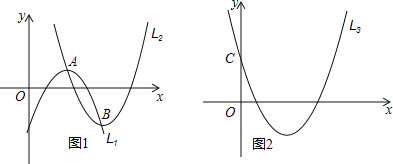
    【题目】如图1，若抛物线L1的顶点A在抛物线L2上，抛物线L2的顶点B也在抛物线L1上（点A与点B不重合）我们把这样的两抛物线L1、L2互称为“友好”抛物线，可见一条抛物线的“友好”抛物线可以有很多条．

    （1）如图2，已知抛物线L3：y=2x2-8x+4与y轴交于点C，试求出点C关于该抛物线对称轴对称的对称点D的坐标；

    （2）请求出以点D为顶点的L3的“友好”抛物线L4的解析式，并指出L3与L4中y同时随x增大而增大的自变量的取值范围；

    （3）若抛物y=a1（x-m）2+n的任意一条“友好”抛物线的解析式为y=a2（x-h）2+k，请写出a1与a2的关系式，并说明理由．

    查看答案和解析>>

    同步练习册答案