
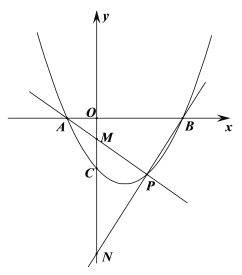
【题目】己知抛物线y=ax2+bx-3a(a>0)与x轴交于A(-1,0)、B两点,与y轴交于点C.
(1)求点B的坐标;
(2)P是第四象限内抛物线上的一个动点.
①若∠APB=90°,且a<3,求点P纵坐标的取值范围;
②直线PA、PB分别交y轴于点M、N求证:![]() 为定值.
为定值.
【答案】(1) B(3,0);(2) ①-2≤n<-![]() ,②
,②![]() =
=![]()
【解析】
(1)把A(-1,0)代入抛物线的解析式,可得a、b的关系,代入取y=0,解方程可得B点坐标.
(2)因为P是第四象限内抛物线上的一个动点.可设设P(m,n), 且m >0, n <0,
①把P(m,n)代入函数解析式,得m、n之间的关系,根据勾股定理列出算式,求出m、n的关系,综合可得到n与a的关系,结合抛物线的顶点坐标及n的取值范围即可确定n的取值范围.
②用待定系数法求直线AP、BP解析式,取x=0求出C、M、N的坐标,表示出CM、CN的长,代入计算即可.
(1)抛物线过A(-1,0)
∴0=a-b-3a,b=-2a,
令y=0,则ax2-2ax-3a=0
a(x2-2x-3)=0, 且a>0
∴B(3,0)
(2)设P(m,n), 且m >0, n <0,则n=am2-2am-3a=a(m2-2m-3).
①AP2=n2+ (m+1)2, BP2=n2+ (3-m)2, AB2=16.
∵∠APB=90°,
∴AP2 +BP2= AB2,即:n2+ (m+1)2+n2+ (3-m)2 =16.
整理后:n2=-m2+2m+3
∴n2=-![]() ,且n <0,
,且n <0,
∴n=-![]() <0
<0
又抛物线顶点(-1,4 a)
∴4a≤-![]() <0,a≥
<0,a≥![]()
又∵a<3
∴![]() ≤a<3
≤a<3
∵-1<0,∴当![]() ≤a<3时,n随a的增大而增大,
≤a<3时,n随a的增大而增大,
∴-2≤n<-![]()
②将x=0代入y=ax2+bx-3a得:y=-3a
∴C(0,-3a)
直线AP过点A(-1,0)、P(m,n)两点,其解析式为:
y=a (m-3)x+ a (m-3),M(0, am-3a)
直线BP过点B(3,0)、P(m,n)两点,其解析式为:
y=a (m+1)x-3a (m+1),N(0, -3am-3a)
∴CM=|-3a-(am-3a)|=| am |
CN=|-3a-(-3am-3a)|=|3am |
∴![]() =
=![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
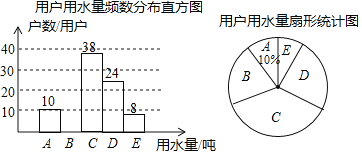
【题目】我市为了节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费为更好地决策,自来水公司在某街道随机抽取了部分用户的用水量数据,按A,B,C,D,E五个区间进行统计,并将统计结果绘制如下两幅不完整的统计图,请你结合图中所给信息解答下列问题:(说明:A:0﹣3吨;B:3﹣6吨;C:6﹣9吨;D:9﹣12吨;E:12﹣16吨,且每组数据区间包括右端的数但不包括左端的数)
(1)这次随机抽样调查了_____用户
(2)补全频数分布直方图,求扇形统计图中B部分的圆心角的度数;
(3)如果自来水公司将基本用水量定为每户9吨,那么该街道1.8万用户中约有多少用户的用水全部享受基本用水量的价格?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司研发生产的560件新产品需要精加工后才能投放市场.现由甲、乙两个工厂来加工生产,已知甲工厂每天加工生产的新产品件数是乙工厂每天加工生产新产品件数的1.5倍,并且加工生产240件新产品甲工厂比乙工厂少用4天.
(1)求甲、乙两个工厂每天分别可加工生产多少件新产品?
(2)若甲工厂每天的加工生产成本为2.8万元,乙工厂每天的加工生产成本为2.4万元要使这批新产品的加工生产总成本不超过60万元,至少应安排甲工厂加工生产多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
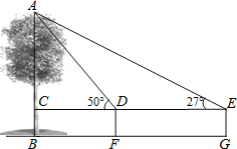
【题目】某数学兴趣小组用高为1.2米的测角仪测量小树AB的高度,如图,在距AB一定距离的F处测得小树顶部A的仰角为50°,沿BF方向行走3.5米到G处时,又测得小树顶部A的仰角为27°,求小树AB的高度.(参考数据:sin27°=0.45,cos27°=0.89,tan27°=0.5,sin50°=0.77,cos50°=0.64,tan50°=1.2)
查看答案和解析>>
科目:初中数学 来源: 题型:
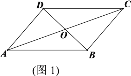
【题目】我们把有两边对应相等,且夹角互补(不相等)的两个三角形叫做“互补三角形”,如图1,□ABCD中,△AOB和△BOC是“互补三角形”.
(1)写出图1中另外一组“互补三角形”_______;
(2)在图2中,用尺规作出一个△EFH,使得△EFH和△EFG为“互补三角形”,且△EFH和△EFG在EF同侧,并证明这一组“互补三角形”的面积相等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在矩形ABCD中,对角线AC与BD相交于点O,过点O作直线EF⊥BD,且交AD于点E,交BC于点F,连接BE,DF,且BE平分∠ABD.
①求证:四边形BFDE是菱形;
②直接写出∠EBF的度数.
(2)把(1)中菱形BFDE进行分离研究,如图2,G,I分别在BF,BE边上,且BG=BI,连接GD,H为GD的中点,连接FH,并延长FH交ED于点J,连接IJ,IH,IF,IG.试探究线段IH与FH之间满足的关系,并说明理由;
(3)把(1)中矩形ABCD进行特殊化探究,如图3,矩形ABCD满足AB=AD时,点E是对角线AC上一点,连接DE,作EF⊥DE,垂足为点E,交AB于点F,连接DF,交AC于点G.请直接写出线段AG,GE,EC三者之间满足的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥CD,∠B=90°,AB=12cm,AD=CD=8cm,动点E从点A出发沿AB以每秒1cm的速度向点B运动,动点F从点B出发沿BA以每秒1cm的速度向点A运动,过点E作AB的垂线交折线AD-DC于点G,以EG、EF为邻边作矩形EFHG,设点E、F运动的时间为t(秒),矩形EFHG与四边形ABCD重叠部分的面积为S(cm2).
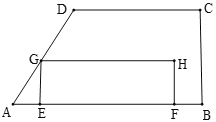
(1)求EG的长(用含t的代数式表示);
(2)当t为何值时,点G与点D重合?
(3)当点G在DC上时,求S(cm2)与t(秒)的函数关系式(S>0);
(4)连接EH、GF、AC、BD,在运动过程中,当这四条线段所在的直线有两条平行时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为更精准地关爱留守学生,某学校将留守学生的各种情形分成四种类型:A.由父母一方照看;B.由爷爷奶奶照看;C.由叔姨等近亲照看;D.直接寄宿学校.某数学小组随机调查了一个班级,发现该班留守学生数量占全班总人数的20%,并将调查结果制成如下两幅不完整的统计图.
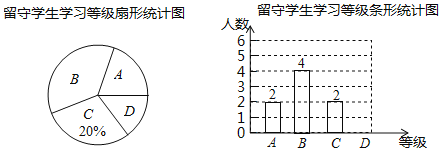
(1)该班共有 名留守学生,B类型留守学生所在扇形的圆心角的度数为 ;
(2)将条形统计图补充完整;
(3)已知该校共有2400名学生,现学校打算对D类型的留守学生进行手拉手关爱活动,请你估计该校将有多少名留守学生在此关爱活动中受益?
查看答案和解析>>
科目:初中数学 来源: 题型:
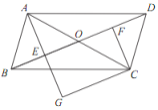
【题目】如图,在□ABCD 中,对角线 AC 与 BD 相交于点 O ,点 E , F 分别为 OB , OD 的中点,延长 AE 至 G ,使 EG =AE ,连接 CG .
(1)求证: △ABE≌△CDF ;
(2)当 AB 与 AC 满足什么数量关系时,四边形 EGCF 是矩形?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com