
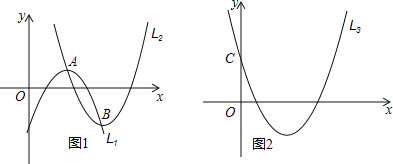
°æƒø°ø»ÁÕº1£¨»Ù≈◊ŒÔœþL1µƒ∂•µ„A‘⁄≈◊ŒÔœþL2…œ£¨≈◊ŒÔœþL2µƒ∂•µ„B“≤‘⁄≈◊ŒÔœþL1…œ£®µ„A”ε„B≤ª÷ÿ∫œ£©Œ“√«∞—’‚—˘µƒ¡Ω≈◊ŒÔœþL1°¢L2ª•≥∆Œ™°∞”—∫√°±≈◊ŒÔœþ£¨ø…º˚“ªÃı≈◊ŒÔœþµƒ°∞”—∫√°±≈◊ŒÔœþø…“‘”–∫Ð∂ýÃı£Æ
£®1£©»ÁÕº2£¨“—÷™≈◊ŒÔœþL3£∫y=2x2-8x+4”Îy÷·Ωª”⁄µ„C£¨ ‘«Û≥ˆµ„Cπÿ”⁄∏√≈◊ŒÔœþ∂‘≥∆÷·∂‘≥∆µƒ∂‘≥∆µ„Dµƒ◊¯±Í£ª
£®2£©«Î«Û≥ˆ“‘µ„DŒ™∂•µ„µƒL3µƒ°∞”—∫√°±≈◊ŒÔœþL4µƒΩ‚Œˆ Ω£¨≤¢÷∏≥ˆL3”ÎL4÷–yÕ¨ ±ÀÊx‘ˆ¥Û∂¯‘ˆ¥Ûµƒ◊‘±‰¡øµƒ»°÷µ∑∂Œß£ª
£®3£©»Ù≈◊ŒÔy=a1£®x-m£©2+nµƒ»Œ“‚“ªÃı°∞”—∫√°±≈◊ŒÔœþµƒΩ‚Œˆ ΩŒ™y=a2£®x-h£©2+k£¨«Î–¥≥ˆa1”Îa2µƒπÿœµ Ω£¨≤¢Àµ√˜¿Ì”…£Æ
°æ¥∞∏°ø£®1£©£®4£¨4£©£ª£®2£©2°Ðx°Ð4£ª£®3£©a1=-a2£¨¿Ì”…»Áœ¬£∫º˚Ω‚Œˆ
°æΩ‚Œˆ°ø
£®1£©…Ëx£Ω0£¨«Û≥ˆyµƒ÷µ£¨º¥ø…µ√µΩCµƒ◊¯±Í£¨∞—≈◊ŒÔœþL3£∫y£Ω2x28x£´4≈‰∑Ωº¥ø…µ√µΩ≈◊ŒÔœþµƒ∂‘≥∆÷·£¨”…¥Àø…«Û≥ˆµ„Cπÿ”⁄∏√≈◊ŒÔœþ∂‘≥∆÷·∂‘≥∆µƒ∂‘≥∆µ„Dµƒ◊¯±Í£ª
£®2£©”…£®1£©ø…÷™µ„Dµƒ◊¯±ÍŒ™£®4£¨4£©£¨‘Ÿ”…Ãıº˛“‘µ„DŒ™∂•µ„µƒL3µƒ°∞”—∫√°±≈◊ŒÔœþL4µƒΩ‚Œˆ Ω£¨ø…«Û≥ˆL4µƒΩ‚Œˆ Ω£¨Ω¯∂¯ø…«Û≥ˆL3”ÎL4÷–yÕ¨ ±ÀÊx‘ˆ¥Û∂¯‘ˆ¥Ûµƒ◊‘±‰¡øµƒ»°÷µ∑∂Œß£ª
£®3£©∏˘æð£∫≈◊ŒÔœþL1µƒ∂•µ„A‘⁄≈◊ŒÔœþL2…œ£¨≈◊ŒÔœþL2µƒ∂•µ„B“≤‘⁄≈◊ŒÔœþL1…œ£¨ø…“‘¡–≥ˆ¡Ω∏ˆ∑Ω≥㨜ýº”ø…µ√£∫£®a1£´a2£©£®mh£©2£Ω0£¨ø…µ√a1£Ωa2.
Ω‚£∫£®1£©°þ≈◊ŒÔœþL3£∫y=2x2-8x+4£¨
°ýy=2£®x-2£©2-4£¨
°ý∂•µ„Œ™£®2£¨4£©£¨∂‘≥∆÷·Œ™x=2£¨
…Ëx=0£¨‘Úy=4£¨
°ýC£®0£¨4£©£¨
°ýµ„Cπÿ”⁄∏√≈◊ŒÔœþ∂‘≥∆÷·∂‘≥∆µƒ∂‘≥∆µ„Dµƒ◊¯±ÍŒ™£∫£®4£¨4£©£ª
£®2£©°þ“‘µ„D£®4£¨4£©Œ™∂•µ„µƒ≈◊ŒÔœþL4π˝µ„£®2£¨-4£©£¨
…ËL4µƒΩ‚Œˆ Ω![]() £¨
£¨
Ω´µ„£®2£¨-4£©¥˙»ÎL4ø…µ√£¨a=-2£¨
°ýL4µƒΩ‚Œˆ ΩŒ™y=-2£®x-4£©2+4£¨
L3”ÎL4µƒ¡Ω∏ˆΩªµ„∑÷±Œ™£®4£¨4£©∫Õ£®2£¨-4£©
°ýL3”ÎL4÷–yÕ¨ ±ÀÊx‘ˆ¥Û∂¯‘ˆ¥Ûµƒ◊‘±‰¡øµƒ»°÷µ∑∂Œß «£∫2°Ðx°Ð4 ±£ª
£®3£©a1=-a2£¨
¿Ì”…»Áœ¬£∫
°þ≈◊ŒÔœþL1µƒ∂•µ„A‘⁄≈◊ŒÔœþL2…œ£¨≈◊ŒÔœþL2µƒ∂•µ„B“≤‘⁄≈◊ŒÔœþL1…œ£¨
°ýø…“‘¡–≥ˆ¡Ω∏ˆ∑Ω≥Ã £¨
£¨
¢Ÿ+¢⁄µ√£∫£®a1+a2£©£®m-h£©2=0£¨
°ýa1=-a2£Æ


 ‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
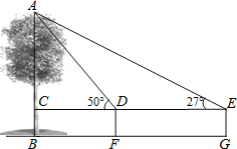
°æƒø°øƒ≥ ˝—ß–À»§–°◊È”√∏þŒ™1.2√◊µƒ≤‚Ω«“«≤‚¡ø–° ˜ABµƒ∏þ∂»£¨»ÁÕº£¨‘⁄æýAB“ª∂®æý¿ÎµƒF¥¶≤‚µ√–° ˜∂•≤øAµƒ—ˆΩ«Œ™50°„£¨—ÿBF∑ΩœÚ––◊þ3.5√◊µΩG¥¶ ±£¨”÷≤‚µ√–° ˜∂•≤øAµƒ—ˆΩ«Œ™27°„£¨«Û–° ˜ABµƒ∏þ∂»£Æ£®≤Œøº ˝æð£∫sin27°„=0.45£¨cos27°„=0.89£¨tan27°„=0.5£¨sin50°„=0.77£¨cos50°„=0.64£¨tan50°„=1.2£©
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒ™∏¸æ´◊ºµÿπÿ∞Æ¡Ù ÿ—ß…˙£¨ƒ≥—ß–£Ω´¡Ù ÿ—ß…˙µƒ∏˜÷÷«È–Œ∑÷≥…Àƒ÷÷¿ý–Õ£∫A£Æ”…∏∏ƒ∏“ª∑Ω’’ø¥£ªB£Æ”…“ؓ؃ÃÒ’ø¥£ªC£Æ”… “õ»Ω¸«◊’’ø¥£ªD£Æ÷±Ω”ºƒÀÞ—ß–££Æƒ≥ ˝—ß–°◊ÈÀʪ˙µ˜≤È¡À“ª∏ˆ∞ýº∂£¨∑¢œ÷∏√∞ý¡Ù ÿ—ß…˙ ˝¡ø’º»´∞ý◊лÀ ˝µƒ20%£¨≤¢Ω´µ˜≤ÈΩ·π˚÷∆≥…»Áœ¬¡Ω∑˘≤ªÕÍ’˚µƒÕ≥º∆Õº£Æ
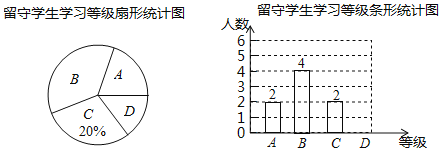
£®1£©∏√∞ýπ≤”–°° °°√˚¡Ù ÿ—ß…˙£¨B¿ý–Õ¡Ù ÿ—ß…˙À˘‘⁄…»–Œµƒ‘≤–ƒΩ«µƒ∂» ˝Œ™°° °°£ª
£®2£©Ω´Ãı–ŒÕ≥º∆Õº≤π≥‰ÕÍ’˚£ª
£®3£©“—÷™∏√–£π≤”–2400√˚—ß…˙£¨œ÷—ß–£¥ÚÀ„∂‘D¿ý–Õµƒ¡Ù ÿ—ß…˙Ω¯–– ÷¿≠ ÷πÿ∞ƪÓ∂Ø£¨«Îƒ„π¿º∆∏√–£Ω´”–∂ý…Ÿ√˚¡Ù ÿ—ß…˙‘⁄¥Àπÿ∞ƪÓ∂Ø÷– Гʣø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
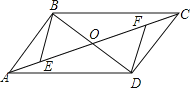
°æƒø°ø»ÁÕº£¨ABCDµƒ∂‘Ω«œþAC°¢BDœýΩª”⁄µ„O£¨OE£ΩOF£Æ
£®1£©«Û÷§£∫°˜BOE°’°˜DOF£ª
£®2£©»ÙBD£ΩEF£¨¡¨Ω”DE°¢BF£¨≈–∂œÀƒ±þ–ŒEBFDµƒ–Œ◊¥£¨≤¢Àµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨µ„A «∑¥±»¿˝∫Ø ˝y£Ω![]() ÕºœÛ…œ“ªµ„£¨π˝µ„A◊˜x÷·µƒ∆Ω––œþΩª∑¥±»¿˝∫Ø ˝y£Ω©Å
ÕºœÛ…œ“ªµ„£¨π˝µ„A◊˜x÷·µƒ∆Ω––œþΩª∑¥±»¿˝∫Ø ˝y£Ω©Å![]() µƒÕºœÛ”⁄µ„B£¨µ„C‘⁄x÷·…œ£¨«“S°˜ABC£Ω
µƒÕºœÛ”⁄µ„B£¨µ„C‘⁄x÷·…œ£¨«“S°˜ABC£Ω![]() £¨‘Úk=£®°°°°£©
£¨‘Úk=£®°°°°£©
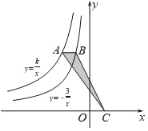
A. 6B. ©Å6C. ![]() D. ©Å
D. ©Å![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨œþ∂Œ AB æ≠π˝°—O µƒ‘≤–ƒ£¨ AC £¨ BD ∑÷±”ΰ—O œý«–”⁄µ„ C £¨D £Æ»Ù AC =BD = 4 £¨°œA=45°„£¨‘Úª°CDµƒ≥§∂»Œ™£® £©
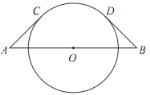
A.¶–B.2¶–C.2![]() ¶–D.4¶–
¶–D.4¶–
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
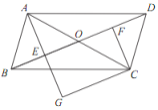
°æƒø°ø»ÁÕº£¨‘⁄°ıABCD ÷–£¨∂‘Ω«œþ AC ”Î BD œýΩª”⁄µ„ O £¨µ„ E £¨ F ∑÷±Œ™ OB £¨ OD µƒ÷–µ„£¨—”≥§ AE ÷¡ G £¨ π EG £ΩAE £¨¡¨Ω” CG £Æ
£®1£©«Û÷§£∫ °˜ABE°’°˜CDF £ª
£®2£©µ± AB ”Î AC ¬˙◊„ ≤√¥ ˝¡øπÿœµ ±£¨Àƒ±þ–Œ EGCF «æÿ–Œ£ø«ÎÀµ√˜¿Ì”….
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒ“ –ƒ≥÷–—ß—ß…˙ª·‘⁄ø™’π°∞¿˜––«⁄ºÛΩ⁄‘º£¨∑¥∂‘∆Ã’≈¿À∑—°±µƒ÷˜Ã‚ΩÔ˝ªÓ∂Ø÷–£¨‘⁄»´–£∑∂Œßƒ⁄Àʪ˙≥È»°¡À»Ù∏…√˚—ß…˙æÕƒ≥»’ÕÌ∑π¿À∑—∑π≤À«ÈøˆΩ¯––µ˜≤È£¨µ˜≤ȃ⁄»ð∑÷Œ™Àƒ÷÷£∫A£Æ∑π∫Õ≤À»´≤ø≥‘ÕÍ£ªB£Æ”– £∑πµ´≤À≥‘ÕÍ£ªC£Æ∑π≥‘Õ͵´≤À”– ££ªD£Æ∑π∫Õ≤À∂º”– ££Æ—ß…˙ª·∏˘æðÕ≥º∆Ω·π˚£¨ªÊ÷∆¡À»Áœ¬Õ≥º∆±Ì£∫∏˘æðÀ˘∏¯–≈œ¢£¨ªÿ¥œ¬¡–Œ £∫
—°œÓ | ∆µ ˝ | ∆µ¬ |
A | 36 | m |
B | n | 0.2 |
C | 6 | 0.1 |
D | 6 | 0.1 |
£®1£©Õ≥º∆±Ì÷–£∫m=______£ªn=______£Æ
£®2£©∏√÷–—ß”–1800√˚—ß…˙ÕÌ∑π‘⁄–£æÕ≤Õ£¨∏˘æðµ˜≤ÈΩ·π˚£¨π¿º∆µ±ÃÏÕÌ∑π”–∂ý…Ÿ»ÀƒÐπª∞—∑π∫Õ≤À»´≤ø≥‘ÕÍ£ø
£®3£©Œ™¡À∂‘Õ¨—ß√«¿À∑—µƒ––Œ™Ω¯––æ¿’˝£¨–£—ß…˙ª·¥”∑π∫Õ≤À∂º”– £µƒº◊°¢““°¢±˚°¢∂°Àƒ√˚Õ¨—ß÷–»Œ»°2ŒªÕ¨—ßΩ¯––≈˙∆¿ΩÔ˝£¨«Î”√¡–±Ì∑®ªÚ ˜◊¥Õº∑®«Û«°∫√≥ÈµΩº◊∫Õ∂°µƒ∏≈¬ £Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄°˜ABC÷–£¨°œACB£Ω90°„£Æ–°¥œÕ¨—ß¿˚”√÷±≥þ∫Õ‘≤πÊÕÍ≥…¡À»Áœ¬◊˜Õº£∫
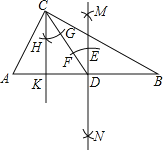
¢Ÿ∑÷±“‘µ„A£¨BŒ™‘≤–ƒ£¨“‘¥Û”⁄![]() AB≥§Œ™∞Îæ∂ª≠ª°£¨¡Ωª°Ωª”⁄µ„M£¨N£¨π˝µ„M£¨N◊˜÷±œþ”ÎABΩª”⁄µ„D£ª
AB≥§Œ™∞Îæ∂ª≠ª°£¨¡Ωª°Ωª”⁄µ„M£¨N£¨π˝µ„M£¨N◊˜÷±œþ”ÎABΩª”⁄µ„D£ª
¢⁄¡¨Ω”CD£¨“‘µ„DŒ™‘≤–ƒ£¨“‘“ª∂®≥§Œ™∞Îæ∂ª≠ª°£¨ΩªMN”⁄µ„E£¨ΩªCD”⁄µ„F£¨“‘µ„CŒ™‘≤–ƒ£¨“‘Õ¨—˘∂®≥§Œ™∞Îæ∂ª≠ª°£¨”ÎCDΩª”⁄µ„G£¨“‘µ„GŒ™‘≤–ƒ£¨“‘EF≥§Œ™∞Îæ∂ª≠ª°”Ϋ∞ª°Ωª”⁄µ„H£Æ◊˜…‰œþCH”ÎABΩª”⁄µ„K£¨«Î∏˘æð“‘…œ≤Ÿ◊˜£¨Ω‚¥œ¬¡–Œ Â
£®1£©”…≥þπÊ◊˜Õºø…÷™£∫÷±œþMN «œþ∂ŒABµƒ°° °°œþ£¨°œDCK£Ω°° °°£Æ
£®2£©»ÙCD£Ω5£¨AK£Ω2£¨«ÛCKµƒ≥§£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com