
【题目】我市某中学学生会在开展“厉行勤俭节约,反对铺张浪费”的主题教育活动中,在全校范围内随机抽取了若干名学生就某日晚饭浪费饭菜情况进行调查,调查内容分为四种:A.饭和菜全部吃完;B.有剩饭但菜吃完;C.饭吃完但菜有剩;D.饭和菜都有剩.学生会根据统计结果,绘制了如下统计表:根据所给信息,回答下列问题:
选项 | 频数 | 频率 |
A | 36 | m |
B | n | 0.2 |
C | 6 | 0.1 |
D | 6 | 0.1 |
(1)统计表中:m=______;n=______.
(2)该中学有1800名学生晚饭在校就餐,根据调查结果,估计当天晚饭有多少人能够把饭和菜全部吃完?
(3)为了对同学们浪费的行为进行纠正,校学生会从饭和菜都有剩的甲、乙、丙、丁四名同学中任取2位同学进行批评教育,请用列表法或树状图法求恰好抽到甲和丁的概率.
科目:初中数学 来源: 题型:
【题目】如图,已知点![]() 和点
和点![]() ,点
,点![]() 和点
和点![]() 是
是![]() 轴上的两个定点.
轴上的两个定点.
(1)当线段![]() 向左平移到某个位置时,若
向左平移到某个位置时,若![]() 的值最小,求平移的距离.
的值最小,求平移的距离.
(2)当线段![]() 向左或向右平移时,是否存在某个位置,使四边形
向左或向右平移时,是否存在某个位置,使四边形![]() 的周长最小?请说明如何平移?若不存在,请说明理由.
的周长最小?请说明如何平移?若不存在,请说明理由.
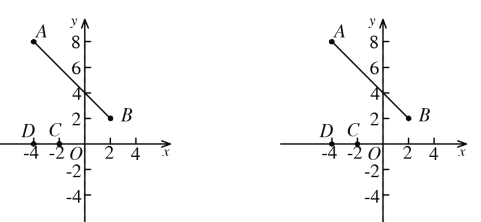
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索与证明:
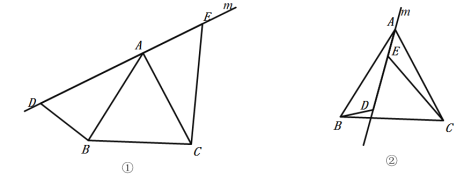
(1)如图①,直线![]() 经过正三角形
经过正三角形![]() 的顶点
的顶点![]() ,在直线
,在直线![]() 上取点
上取点![]() ,
,![]() ,使得
,使得![]() ,
,![]() .通过观察或测量,猜想线段
.通过观察或测量,猜想线段![]() ,
,![]() 与
与![]() 之间满足的数量关系,并予以证明;
之间满足的数量关系,并予以证明;
(2)将(1)中的直线![]() 绕着点
绕着点![]() 逆时针方向旋转一个角度到如图②的位置,
逆时针方向旋转一个角度到如图②的位置,![]() ,
,![]() .通过观察或测量,猜想线段
.通过观察或测量,猜想线段![]() ,
,![]() 与
与![]() 之间满足的数量关系,并予以证明.
之间满足的数量关系,并予以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 和
和![]() 都是等腰直角角三角角形;
都是等腰直角角三角角形;![]() ,点
,点![]() 是直线
是直线![]() 上的一动点(点
上的一动点(点![]() 不与
不与![]() 、
、![]() 重合),连接
重合),连接![]() .
.
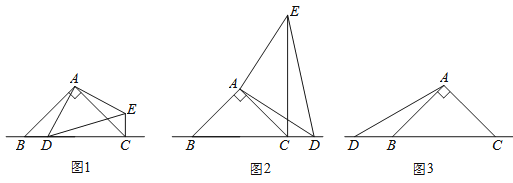
(1)在图1中,当点![]() 在边
在边![]() 上时,求证:①
上时,求证:①![]() ;②
;②![]() ;
;
(2)在图2中,当点![]() 在边
在边![]() 的廷长线上时,结论①
的廷长线上时,结论①![]() 是否还成立?若不成立,请直接写出
是否还成立?若不成立,请直接写出![]() 之间存在的数量关系,不必说明理由.
之间存在的数量关系,不必说明理由.
(3)在图3中当点![]() 在边
在边![]() 的反向延长线上时,补全图形,不写证明过程,直接写出
的反向延长线上时,补全图形,不写证明过程,直接写出![]() 之间存在的数量关系.
之间存在的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
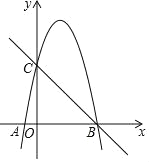
【题目】如图,抛物线y=﹣x2+4x+5与x轴,y轴分别交于A,B,C三点.
(1)请直接写出A,B,C三点坐标:A(_____,_____)、B(_____,______)、C(______,______)
(2)若⊙M过A、B、C三点,求圆心M的坐标,并求⊙M的面积;
(3)在(2)的条件下,在抛物线上是否存在点N,使得由A,C,M,N四点构成的四边形为平行四边形?若存在,请求出点N的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 和
和![]() 中,
中,![]() 连接AC,BD交于点M,AC与OD相交于E,BD与OA相较于F,连接OM,则下列结论中:①
连接AC,BD交于点M,AC与OD相交于E,BD与OA相较于F,连接OM,则下列结论中:①![]() ;②
;②![]() ;③
;③![]() ;④MO平分
;④MO平分![]() ,正确的个数有( )
,正确的个数有( )
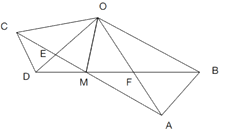
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
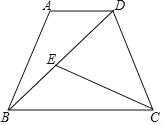
【题目】在梯形ABCD中,AD∥BC,AB=CD,BD=BC,点E在对角线BD上,且∠DCE=∠DBC.
(1)求证:AD=BE;
(2)延长CE交AB于点F,如果CF⊥AB,求证:4EFFC=DEBD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学生在素质教育基地进行社会实践活动,帮助农民伯伯采摘了黄瓜和茄子共40kg,了解到这些蔬菜的种植成本共42元,还了解到如下信息:黄瓜的种植成本是1元/kg,售价为1.5元/kg;茄子的种植成本是1.2元/kg,售价是2元/kg.
(1)请问采摘的黄瓜和茄子各多少千克?
(2)这些采摘的黄瓜和茄子可赚多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com