
【题目】已知![]() 和
和![]() 都是等腰直角角三角角形;
都是等腰直角角三角角形;![]() ,点
,点![]() 是直线
是直线![]() 上的一动点(点
上的一动点(点![]() 不与
不与![]() 、
、![]() 重合),连接
重合),连接![]() .
.
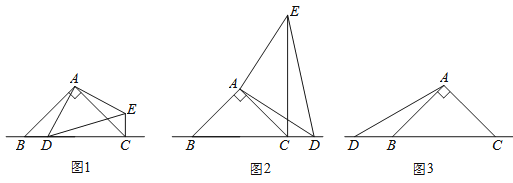
(1)在图1中,当点![]() 在边
在边![]() 上时,求证:①
上时,求证:①![]() ;②
;②![]() ;
;
(2)在图2中,当点![]() 在边
在边![]() 的廷长线上时,结论①
的廷长线上时,结论①![]() 是否还成立?若不成立,请直接写出
是否还成立?若不成立,请直接写出![]() 之间存在的数量关系,不必说明理由.
之间存在的数量关系,不必说明理由.
(3)在图3中当点![]() 在边
在边![]() 的反向延长线上时,补全图形,不写证明过程,直接写出
的反向延长线上时,补全图形,不写证明过程,直接写出![]() 之间存在的数量关系.
之间存在的数量关系.
【答案】(1)见解析(2)CE=BC+CD,理由见解析(3)CD=BC+EC,理由见解析
【解析】
(1)只要证明△ABD≌△ACE(SAS),可得BD=CE,即可推出BC=BD+CD=EC+CD,再得到∠ECD=90![]() 即可求解;
即可求解;
(2)不成立,存在的数量关系为CE=BC+CD,利用全等三角形的性质即可证明;
(3)根据题意补全图形,同(1)可证明△ABD≌△ACE即可求解.
(1)∵AB=AC,∠ABC=∠ACB=45![]() ,AD=AE,∠ADE=∠AED=45
,AD=AE,∠ADE=∠AED=45![]() ,
,
∴∠BAC=∠DAE=90![]() ,
,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
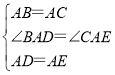 ,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,
∴BC=BD+CD=CE+CD;
∴∠ACE=∠ABD=45![]()
∴∠ECD=∠ACE +∠ACB =90![]()
∴![]()
(2)不成立,存在的数量关系为CE=BC+CD.
理由:由(1)同理可得,
在△ABD和△ACE中,
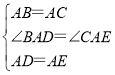 ,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,
∴BD=BC+CD,
∴CE=BC+CD;
(3)如图3,结论:CD=BC+EC.
依题意补全图形,
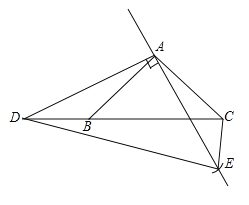
理由:由(1)同理可得,
在△ABD和△ACE中,
 ,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,
∴CD=BC+BD=BC+CE.


科目:初中数学 来源: 题型:
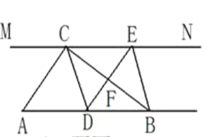
【题目】如图,在Rt△ABC中,∠ACB=90,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE
(1)求证:CE=AD
(2)当点D在AB中点时,四边形BECD是什么特殊四边形?说明理由
(3)若D为AB的中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 在平面直角坐标系中的位置如图所示.
在平面直角坐标系中的位置如图所示.

(1)作出![]() 关于
关于![]() 轴对称的
轴对称的![]() ,并写出
,并写出![]() 各顶点的坐标;
各顶点的坐标;
(2)将![]() 向右平移6个单位,作出平移后的
向右平移6个单位,作出平移后的![]() 并写出
并写出![]() 各顶点的坐标;
各顶点的坐标;
(3)观察![]() 和
和![]() ,它们是否关于某直线对称?若是,请用粗线条画出对称轴.
,它们是否关于某直线对称?若是,请用粗线条画出对称轴.
查看答案和解析>>
科目:初中数学 来源: 题型:
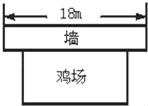
【题目】如图某农场要建一个长方形的养鸡场,鸡场的一边靠墙(墙长18m),另三边用木栏围成,木栏长35m.鸡场的面积能达到150m2吗?如果能,请你给出设计方案;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个拱形桥架可以近似看作是由等腰梯形ABD8D1和其上方的抛物线D1OD8组成.若建立如图所示的直角坐标系,跨度AB=44米,∠A=45°,AC1=4米,点D2的坐标为(-13,-1.69),则桥架的拱高OH=________米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=﹣![]() x2+bx+c的图象经过A(2,0),B(0,﹣6)两点,
x2+bx+c的图象经过A(2,0),B(0,﹣6)两点,
(1)求这个二次函数的解析式;
(2)设该二次函数的对称轴与x轴交于点C,连接BA,BC,求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学学生会在开展“厉行勤俭节约,反对铺张浪费”的主题教育活动中,在全校范围内随机抽取了若干名学生就某日晚饭浪费饭菜情况进行调查,调查内容分为四种:A.饭和菜全部吃完;B.有剩饭但菜吃完;C.饭吃完但菜有剩;D.饭和菜都有剩.学生会根据统计结果,绘制了如下统计表:根据所给信息,回答下列问题:
选项 | 频数 | 频率 |
A | 36 | m |
B | n | 0.2 |
C | 6 | 0.1 |
D | 6 | 0.1 |
(1)统计表中:m=______;n=______.
(2)该中学有1800名学生晚饭在校就餐,根据调查结果,估计当天晚饭有多少人能够把饭和菜全部吃完?
(3)为了对同学们浪费的行为进行纠正,校学生会从饭和菜都有剩的甲、乙、丙、丁四名同学中任取2位同学进行批评教育,请用列表法或树状图法求恰好抽到甲和丁的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
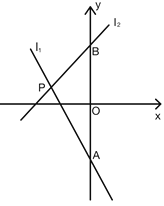
【题目】如图,已知直线![]() ,直线
,直线![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() 分别与
分别与![]() 轴相交于点
轴相交于点![]() .
.
(1)求点P的坐标.
(2)若![]() ,求x的取值范围.
,求x的取值范围.
(3)点![]() 为x轴上的一个动点,过
为x轴上的一个动点,过![]() 作x轴的垂线分别交
作x轴的垂线分别交![]() 和
和![]() 于点
于点![]() ,当EF=3时,求m的值.
,当EF=3时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
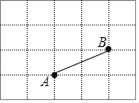
【题目】如图,在每个小正方形的边长为1的网格中,A,B为格点
(Ⅰ)AB的长等于__
(Ⅱ)请用无刻度的直尺,在如图所示的网格中求作一点C,使得CA=CB且△ABC的面积等于![]() ,并简要说明点C的位置是如何找到的__________________
,并简要说明点C的位置是如何找到的__________________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com