
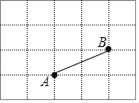
【题目】如图,在每个小正方形的边长为1的网格中,A,B为格点
(Ⅰ)AB的长等于__
(Ⅱ)请用无刻度的直尺,在如图所示的网格中求作一点C,使得CA=CB且△ABC的面积等于![]() ,并简要说明点C的位置是如何找到的__________________
,并简要说明点C的位置是如何找到的__________________
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
【题目】已知![]() 和
和![]() 都是等腰直角角三角角形;
都是等腰直角角三角角形;![]() ,点
,点![]() 是直线
是直线![]() 上的一动点(点
上的一动点(点![]() 不与
不与![]() 、
、![]() 重合),连接
重合),连接![]() .
.
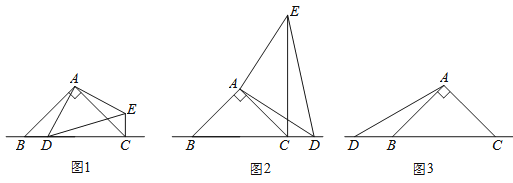
(1)在图1中,当点![]() 在边
在边![]() 上时,求证:①
上时,求证:①![]() ;②
;②![]() ;
;
(2)在图2中,当点![]() 在边
在边![]() 的廷长线上时,结论①
的廷长线上时,结论①![]() 是否还成立?若不成立,请直接写出
是否还成立?若不成立,请直接写出![]() 之间存在的数量关系,不必说明理由.
之间存在的数量关系,不必说明理由.
(3)在图3中当点![]() 在边
在边![]() 的反向延长线上时,补全图形,不写证明过程,直接写出
的反向延长线上时,补全图形,不写证明过程,直接写出![]() 之间存在的数量关系.
之间存在的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
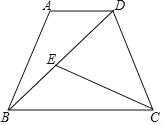
【题目】在梯形ABCD中,AD∥BC,AB=CD,BD=BC,点E在对角线BD上,且∠DCE=∠DBC.
(1)求证:AD=BE;
(2)延长CE交AB于点F,如果CF⊥AB,求证:4EFFC=DEBD.
查看答案和解析>>
科目:初中数学 来源: 题型:
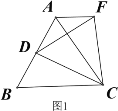
【题目】操作发现:如图1,D是等边△ABC边BA上的一动点(点D与点B不重合),连接DC,以DC为边在BC上方作等边△DCF,连接AF,易证AF=BD(不需要证明);
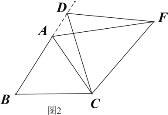
类比猜想:①如图2,当动点D运动至等边△ABC边BA的延长线上时,其它作法与图1相同,猜想AF与BD在图1中的结论是否仍然成立。
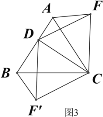
深入探究:②如图3,当动点D在等边△ABC边BA上的一动点(点D与点B不重合),连接DC,以DC为边在BC上方、下方分别作等边△DCF和等边△DCF′,连接AF,BF′你能发现AF,BF′与AB有何数量关系,并证明你发现的结论。
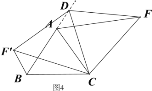
③如图4,当动点D运动至等边△ABC边BA的延长线上时,其它作法与图3相同,猜想AF,BF′与AB在上题②中的结论是否仍然成立,若不成立,请给出你的结论并证明。
查看答案和解析>>
科目:初中数学 来源: 题型:
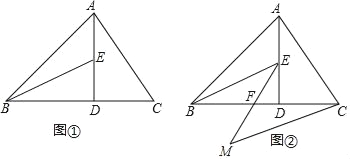
【题目】问题原型:如图①,在锐角△ABC中,∠ABC=45°,AD⊥BC于点D,在AD上取点E,使DE=CD,连结BE.求证:BE=AC.
问题拓展:如图②,在问题原型的条件下,F为BC的中点,连结EF并延长至点M,使FM=EF,连结CM.
(1)判断线段AC与CM的大小关系,并说明理由.
(2)若AC=![]() ,直接写出A、M两点之间的距离.
,直接写出A、M两点之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
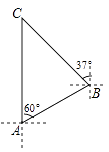
【题目】知识改变世界,科技改变生活.导航装备的不断更新极大方便了人们的出行.如图,某校组织学生乘车到黑龙滩(用C表示)开展社会实践活动,车到达A地后,发现C地恰好在A地的正北方向,且距离A地13千米,导航显示车辆应沿北偏东60°方向行驶至B地,再沿北偏西37°方向行驶一段距离才能到达C地,求B、C两地的距离.(参考数据:sin53°≈![]() ,cos53°≈
,cos53°≈![]() ,tan53°≈
,tan53°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学生在素质教育基地进行社会实践活动,帮助农民伯伯采摘了黄瓜和茄子共40kg,了解到这些蔬菜的种植成本共42元,还了解到如下信息:黄瓜的种植成本是1元/kg,售价为1.5元/kg;茄子的种植成本是1.2元/kg,售价是2元/kg.
(1)请问采摘的黄瓜和茄子各多少千克?
(2)这些采摘的黄瓜和茄子可赚多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一块直角三角形纸片,两直角边AB=6,BC=8,将△ABC折叠,使AB落在斜边AC上,折痕为AD,则BD的长为( )

A. 6B. 5C. 4D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com