
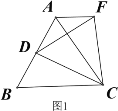
【题目】操作发现:如图1,D是等边△ABC边BA上的一动点(点D与点B不重合),连接DC,以DC为边在BC上方作等边△DCF,连接AF,易证AF=BD(不需要证明);
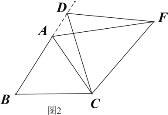
类比猜想:①如图2,当动点D运动至等边△ABC边BA的延长线上时,其它作法与图1相同,猜想AF与BD在图1中的结论是否仍然成立。
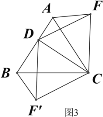
深入探究:②如图3,当动点D在等边△ABC边BA上的一动点(点D与点B不重合),连接DC,以DC为边在BC上方、下方分别作等边△DCF和等边△DCF′,连接AF,BF′你能发现AF,BF′与AB有何数量关系,并证明你发现的结论。
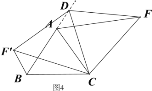
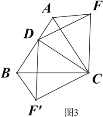
③如图4,当动点D运动至等边△ABC边BA的延长线上时,其它作法与图3相同,猜想AF,BF′与AB在上题②中的结论是否仍然成立,若不成立,请给出你的结论并证明。
【答案】①成立,证明见详解;②AF+BF′=AB,证明见详解;③不成立,AF=AB+BF′,证明见详解.
【解析】
类比猜想:①通过证明△BCD≌△ACF,即可证明AF=BD;
深入探究:②AF+BF′=AB,利用全等三角形△BCD≌△ACF(SAS)的对应边BD=AF;同理△BCF′≌△ACD(SAS),则BF′=AD,所以AF+BF′=AB;
③结论不成立.新的结论是AF=AB+BF′;通过证明△BCF′≌△ACD(SAS),则BF′=AD(全等三角形的对应边相等);再结合(2)中的结论即可证得AF=AB+BF′.
解:类比猜想:①如图2中,
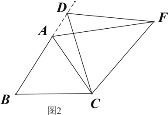
∵△ABC是等边三角形(已知),
∴BC=AC,∠BCA=60°(等边三角形的性质);
同理知,DC=CF,∠DCF=60°;
∴∠BCA+∠DCA=∠DCF+∠DCA,即∠BCD=∠ACF;
在△BCD和△ACF中,
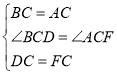
∴△BCD≌△ACF(SAS),
∴BD=AF(全等三角形的对应边相等);
深入探究:②如图示
AF+BF′=AB;
证明如下:由①条件可知:∠BCA-∠DCA=∠DCF-∠DCA,即∠BCD=∠ACF,
∴同理可证△BCD≌△ACF(SAS),则BD=AF;
同理△BCF′≌△ACD(SAS),则BF′=AD,
∴AF+BF′=BD+AD=AB;
③结论不成立.新的结论是AF=AB+BF′;
如图示:
证明如下:
∵等边△DCF和等边△DCF′,由①同理可知:
在△BCF′和△ACD中,
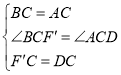
∴△BCF′≌△ACD(SAS),
∴BF′=AD(全等三角形的对应边相等);
又由②知,AF=BD;
∴AF=BD=AB+AD=AB+BF′,即AF=AB+BF′.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】自学下面材料后,解答问题.
分母中含有未知数的不等式叫分式不等式.如:![]() ;
;![]() <0等.那么如何求出它们的解集呢?
<0等.那么如何求出它们的解集呢?
根据我们学过的有理数除法法则可知:两数相除,同号得正,异号得负.其字母表达式为:
(1)若a>0,b>0,则![]() >0;若a<0,b<0,则
>0;若a<0,b<0,则![]() >0;
>0;
(2)若a>0,b<0,则![]() <0;若a<0,b>0,则
<0;若a<0,b>0,则![]() <0.
<0.
反之:(1)若![]() >0,则
>0,则![]() 或
或![]()
(2)若![]() <0,则 或 .
<0,则 或 .
根据上述规律,求不等式![]() >0的解集.
>0的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,对称轴为直线![]() 的抛物线
的抛物线![]() 与x轴相交于A、B两点,其中A点的坐标为(-3,0)。
与x轴相交于A、B两点,其中A点的坐标为(-3,0)。

(1)求点B的坐标;
(2)已知![]() ,C为抛物线与y轴的交点。
,C为抛物线与y轴的交点。
①若点P在抛物线上,且![]() ,求点P的坐标;
,求点P的坐标;
②设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强语文课外阅读,某年级积极组织学生参加课外阅读读书分享会活动.从年级推荐的四种读物A:《水浒传》、B:《骆驼祥子》、C:《昆虫记》、D:《朝花夕拾》中选择一本读物每周一与班级同学分享读书体会。读书分享会活动组随机抽取本年级的部分学生,调查他们这四本读物中最喜爱一本读物,并将调查结果绘制成如下两幅不完整的统计图,请你结合图中的信息解答下列问题:

(1)求被调查的学生人数;
(2)补全条形统计图;
(3)已知该年级有![]() 名学生,估计全年级最喜爱《水浒传》的学生有多少人?
名学生,估计全年级最喜爱《水浒传》的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB的垂直平分线分别交AB,BC于点D,E,∠B=30°,∠BAC=80°,且BC+AC=12cm,①求∠CAE的度数;②求△AEC的周长。
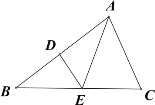
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.以AB上某一点O为圆心作⊙O,使⊙O经过点A和点D.
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若AC=3,∠B=30°.
①求⊙O的半径;
②设⊙O与AB边的另一个交点为E,求线段BD、BE与劣弧DE所围成的阴影部分的图形面积.(结果保留根号和π)
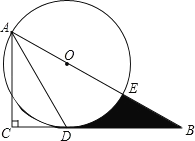
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在正方形ABCD中,P是对角线AC上的一点,点E在BC的延长线上,且PE=PB.

(1)求证:△BCP≌△DCP;
(2)求证:∠DPE=∠ABC;
(3)把正方形ABCD改为菱形,其它条件不变(如图②),若∠ABC=58°,则∠DPE= 度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数y=![]() (k≠0)与一次函数y=mx+b(m≠0)交于点A(1,2k﹣1).
(k≠0)与一次函数y=mx+b(m≠0)交于点A(1,2k﹣1).
(1)求反比例函数的解析式;
(2)若一次函数与x轴交于点B,且△AOB的面积为3,求一次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究问题:已知![]() ,画一个角
,画一个角![]() ,使
,使![]() ,且
,且![]() 交
交![]() 于点
于点![]() .
.![]() 与
与![]() 有怎样的数量关系?
有怎样的数量关系?

(1)我们发现![]() 与
与![]() 有两种位置关系:如图1与图2所示.
有两种位置关系:如图1与图2所示.
①图1中![]() 与
与![]() 数量关系为____________;图2中
数量关系为____________;图2中![]() 与
与![]() 数量关系为____________.请选择其中一种情况说明理由.
数量关系为____________.请选择其中一种情况说明理由.
②由①得出一个真命题(用文字叙述):____________________________.
(2)应用②中的真命题,解决以下问题:若两个角的两边互相平行,且一个角比另一个角的2倍少30°,请直接写出这两个角的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com