
【题目】反比例函数y=![]() (k≠0)与一次函数y=mx+b(m≠0)交于点A(1,2k﹣1).
(k≠0)与一次函数y=mx+b(m≠0)交于点A(1,2k﹣1).
(1)求反比例函数的解析式;
(2)若一次函数与x轴交于点B,且△AOB的面积为3,求一次函数的解析式.
【答案】(1)y=![]() ;(2)y=﹣
;(2)y=﹣![]() 或y=
或y=![]()
【解析】
试题(1)把A(1,2k-1)代入y=![]() 即可求得结果;
即可求得结果;
(2)根据三角形的面积等于3,求得点B的坐标,代入一次函数y=mx+b即可得到结果.
试题解析:
(1)把A(1,2k﹣1)代入y=![]() 得,
得,
2k﹣1=k,
∴k=1,
∴反比例函数的解析式为:y=![]() ;
;
(2)由(1)得k=1,
∴A(1,1),
设B(a,0),
∴S△AOB=![]() |a|×1=3,
|a|×1=3,
∴a=±6,
∴B(﹣6,0)或(6,0),
把A(1,1),B(﹣6,0)代入y=mx+b得:
![]() ,
,
∴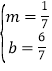 ,
,
∴一次函数的解析式为:y=![]() x+
x+![]() ,
,
把A(1,1),B(6,0)代入y=mx+b得:
![]() ,
,
∴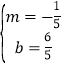 ,
,
∴一次函数的解析式为:y=﹣![]() .
.
所以符合条件的一次函数解析式为:y=﹣![]() 或y=
或y=![]() x+
x+![]() .
.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数![]() 的图象经过点A(﹣3,﹣2).
的图象经过点A(﹣3,﹣2).
(1)求反比例函数的解析式;
(2)若点B(1,m),C(3,n)在该函数的图象上,试比较m与n的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
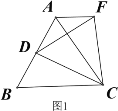
【题目】操作发现:如图1,D是等边△ABC边BA上的一动点(点D与点B不重合),连接DC,以DC为边在BC上方作等边△DCF,连接AF,易证AF=BD(不需要证明);
类比猜想:①如图2,当动点D运动至等边△ABC边BA的延长线上时,其它作法与图1相同,猜想AF与BD在图1中的结论是否仍然成立。
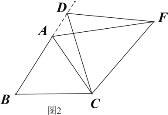
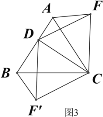
深入探究:②如图3,当动点D在等边△ABC边BA上的一动点(点D与点B不重合),连接DC,以DC为边在BC上方、下方分别作等边△DCF和等边△DCF′,连接AF,BF′你能发现AF,BF′与AB有何数量关系,并证明你发现的结论。
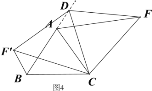
③如图4,当动点D运动至等边△ABC边BA的延长线上时,其它作法与图3相同,猜想AF,BF′与AB在上题②中的结论是否仍然成立,若不成立,请给出你的结论并证明。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC的度数为( )
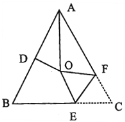
A.120°B.108°C.110°D.102°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线p: ![]() 的顶点为C,与x轴相交于A、B两点(点A在点B左侧),点C关于x轴的对称点为C′,我们称以A为顶点且过点C′,对称轴与y轴平行的抛物线为抛物线p的“梦之星”抛物线,直线AC′为抛物线p的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是
的顶点为C,与x轴相交于A、B两点(点A在点B左侧),点C关于x轴的对称点为C′,我们称以A为顶点且过点C′,对称轴与y轴平行的抛物线为抛物线p的“梦之星”抛物线,直线AC′为抛物线p的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是![]() 和y=2x+2,则这条抛物线的解析式为____________________.
和y=2x+2,则这条抛物线的解析式为____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2016CCTV英语风采大赛中,娄底市参赛选手表现突出,成绩均不低于60分.为了更好地了解娄底赛区的成绩分布情况,随机抽取利了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行了整理,得到如图的两幅不完整的统计图表:
根据所给信息,解答下列问题:
(1)在表中的频数分布表中,m= ,n= .
成绩 | 频数 | 频率 |
60≤x<70 | 60 | 0.30 |
70≤x<80 | m | 0.40 |
80≤x<90 | 40 | n |
90≤x≤100 | 20 | 0.10 |
(2)请补全图中的频数分布直方图.

(3)按规定,成绩在80分以上(包括80分)的选手进入决赛.若娄底市共有4000人参数,请估计约有多少人进入决赛?
查看答案和解析>>
科目:初中数学 来源: 题型:
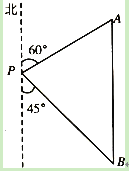
【题目】五一期间,小红到美丽的世界地质公园湖光岩参加社会实践活动,在景点P处测得景点B位于南偏东45°方向;然后沿北偏东60°方向走100米到达景点A,此时测得景点B正好位于景点A的正南方向,求景点A与B之间的距离.(结果精确到0.1米)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com