
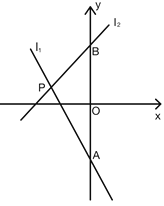
【题目】如图,已知直线![]() ,直线
,直线![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() 分别与
分别与![]() 轴相交于点
轴相交于点![]() .
.
(1)求点P的坐标.
(2)若![]() ,求x的取值范围.
,求x的取值范围.
(3)点![]() 为x轴上的一个动点,过
为x轴上的一个动点,过![]() 作x轴的垂线分别交
作x轴的垂线分别交![]() 和
和![]() 于点
于点![]() ,当EF=3时,求m的值.
,当EF=3时,求m的值.
【答案】(1)P(-2,1);(2)-3<x<-2;(3)m=-3或m=-1.
【解析】
(1)由点P是两直线的交点,则由两方程的函数值相等,解出x,即可得到点P坐标;
(2)由![]() ,联立成不等式组,解不等式组即可得到x的取值范围;
,联立成不等式组,解不等式组即可得到x的取值范围;
(3)由点D的横坐标为m,结合EF=3,可分为两种情况进行讨论:点D在点P的左边;点D在点P的右边,分别计算,即可得到m的值.
解:(1)P点是直线l1与直线l2的交点,可得:![]() 2x
2x![]() 3=x+3,
3=x+3,
解得:x=![]() 2 ,
2 ,
∴y=1;
∴ P点的坐标为:(![]() 2,1);
2,1);
(3)![]() ,
,
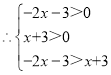 ,解得:
,解得: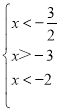 ;
;
![]() ;
;
(3)∵点D为(m,0),根据题意可知,
则E(m,![]() 2m
2m![]() 3);F(m,m+3),
3);F(m,m+3),
第一种情况:点D在点P的左边时,此时点E在点F的上方;
∴![]() ,
,
![]() ;
;
第二种情况:点D在点P的右边时,此时点E在点F的下方;
∴![]() ,
,
![]() ;
;
∴m的值为:![]() 或
或![]() .
.


 小学教材全测系列答案
小学教材全测系列答案科目:初中数学 来源: 题型:
【题目】如图1,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于
轴交于![]() 、
、![]() 两点,
两点,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,点
,点![]() 为线段
为线段![]() 上一点,过点
上一点,过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,已知
,已知![]() ,
,![]() ,且
,且![]() 满足
满足![]() .
.
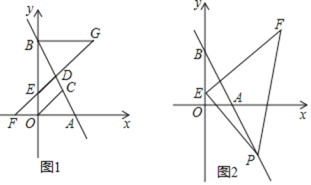
(1)求![]() 两点的坐标;
两点的坐标;
(2)若点![]() 为
为![]() 中点,延长
中点,延长![]() 交
交![]() 轴于点
轴于点![]() ,在
,在![]() 的延长线上取点
的延长线上取点![]() ,使
,使![]() ,连接
,连接![]() .
.
①![]() 与
与![]() 轴的位置关系怎样?说明理由;
轴的位置关系怎样?说明理由;
②求![]() 的长;
的长;
(3)如图2,若点![]() 的坐标为
的坐标为![]() ,
,![]() 是
是![]() 轴的正半轴上一动点,
轴的正半轴上一动点,![]() 是直线
是直线![]() 上一点,且
上一点,且![]() 的坐标为
的坐标为![]() ,是否存在点
,是否存在点![]() 使
使![]() 为等腰直角三角形?若存在,求出点
为等腰直角三角形?若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
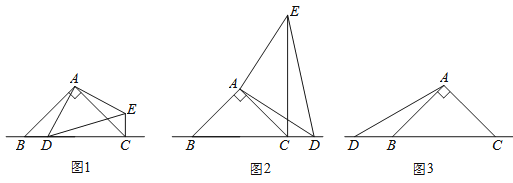
【题目】已知![]() 和
和![]() 都是等腰直角角三角角形;
都是等腰直角角三角角形;![]() ,点
,点![]() 是直线
是直线![]() 上的一动点(点
上的一动点(点![]() 不与
不与![]() 、
、![]() 重合),连接
重合),连接![]() .
.
(1)在图1中,当点![]() 在边
在边![]() 上时,求证:①
上时,求证:①![]() ;②
;②![]() ;
;
(2)在图2中,当点![]() 在边
在边![]() 的廷长线上时,结论①
的廷长线上时,结论①![]() 是否还成立?若不成立,请直接写出
是否还成立?若不成立,请直接写出![]() 之间存在的数量关系,不必说明理由.
之间存在的数量关系,不必说明理由.
(3)在图3中当点![]() 在边
在边![]() 的反向延长线上时,补全图形,不写证明过程,直接写出
的反向延长线上时,补全图形,不写证明过程,直接写出![]() 之间存在的数量关系.
之间存在的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
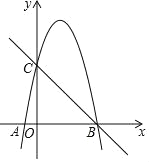
【题目】如图,抛物线y=﹣x2+4x+5与x轴,y轴分别交于A,B,C三点.
(1)请直接写出A,B,C三点坐标:A(_____,_____)、B(_____,______)、C(______,______)
(2)若⊙M过A、B、C三点,求圆心M的坐标,并求⊙M的面积;
(3)在(2)的条件下,在抛物线上是否存在点N,使得由A,C,M,N四点构成的四边形为平行四边形?若存在,请求出点N的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 和
和![]() 中,
中,![]() 连接AC,BD交于点M,AC与OD相交于E,BD与OA相较于F,连接OM,则下列结论中:①
连接AC,BD交于点M,AC与OD相交于E,BD与OA相较于F,连接OM,则下列结论中:①![]() ;②
;②![]() ;③
;③![]() ;④MO平分
;④MO平分![]() ,正确的个数有( )
,正确的个数有( )
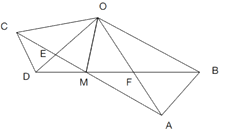
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.

(1)求证:△DEF是等腰三角形;
(2)当∠A=36°时,求∠DEF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
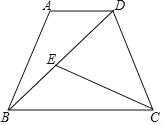
【题目】在梯形ABCD中,AD∥BC,AB=CD,BD=BC,点E在对角线BD上,且∠DCE=∠DBC.
(1)求证:AD=BE;
(2)延长CE交AB于点F,如果CF⊥AB,求证:4EFFC=DEBD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作发现:如图1,D是等边△ABC边BA上的一动点(点D与点B不重合),连接DC,以DC为边在BC上方作等边△DCF,连接AF,易证AF=BD(不需要证明);
类比猜想:①如图2,当动点D运动至等边△ABC边BA的延长线上时,其它作法与图1相同,猜想AF与BD在图1中的结论是否仍然成立。
深入探究:②如图3,当动点D在等边△ABC边BA上的一动点(点D与点B不重合),连接DC,以DC为边在BC上方、下方分别作等边△DCF和等边△DCF′,连接AF,BF′你能发现AF,BF′与AB有何数量关系,并证明你发现的结论。
③如图4,当动点D运动至等边△ABC边BA的延长线上时,其它作法与图3相同,猜想AF,BF′与AB在上题②中的结论是否仍然成立,若不成立,请给出你的结论并证明。
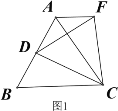
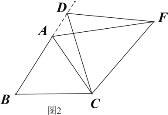
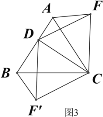
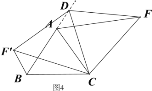
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com