
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.

(1)求证:△DEF是等腰三角形;
(2)当∠A=36°时,求∠DEF的度数.
【答案】(1)详见解析;(2)72°.
【解析】
(1)根据AB=AC可得∠B=∠C,即可求证△BDE≌△CEF,即可解题;
(2)根据全等三角形的性质得到∠CEF=∠BDE,于是得到∠DEF=∠B,根据等腰三角形的性质结合三角形内角和定理即可得出结果
解:(1)∵AB=AC,
∴∠B=∠C,
在△BDE和△CEF中,
 ,
,
∴△BDE≌△CEF(SAS),
∴DE=EF,
∴△DEF是等腰三角形;
(2)∵∠DEC=∠B+∠BDE,
即∠DEF+∠CEF=∠B+∠BDE,
∵△BDE≌△CEF,
∴∠CEF=∠BDE,
∴∠DEF=∠B,
又∵在△ABC中,AB=AC,∠A=36°,
∴∠B=![]() ,
,
∴∠DEF=72°.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 是线段
是线段![]() 上的一点,以
上的一点,以![]() 为腰在第二象限内作等腰直角
为腰在第二象限内作等腰直角![]() ,
,![]() .
.

(1)请直接写出点![]() ,
,![]() 的坐标:
的坐标:![]() ( , ),
( , ),![]() ( , );
( , );
(2)设点![]() 的坐标为
的坐标为![]() ,连接
,连接![]() 并延长交
并延长交![]() 轴于点
轴于点![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形![]() 的边长为4,
的边长为4,![]() 为边
为边![]() 上一点,过点
上一点,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,在
,在![]() 右侧作等边三角形
右侧作等边三角形![]() ,记
,记![]() 到
到![]() 的距离为
的距离为![]() ,
,![]() 到
到![]() 的距离为
的距离为![]() ,
,
(1)若![]() ,试求线段
,试求线段![]() 的长,并求m1、m2的值.
的长,并求m1、m2的值.
(2)若![]() ,用含
,用含![]() 的代数式表示
的代数式表示![]() ,
,![]() ,并求
,并求![]() 在∠C的平分线上时x的值.
在∠C的平分线上时x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是∠AOB内任意一点,且∠AOB=40°,点M和点N分别是射线OA和射线OB上的动点,当△PMN周长取最小值时,则∠MPN的度数为( )

A. 140° B. 100° C. 50° D. 40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C是线段AB上一点,分别以AC和BC为边在线段AB的同侧作等边△ACD和△BCE,连结AE和BD,相交于点F.
(1)求证:AE=BD;
(2)如图2.固定△BCE不动,将等边△ACD绕点C旋转(△ACD和△BCE不重叠),试问∠AFB的大小是否变化?请说明理由;
(3)在△ACD旋转的过程中,以下结论:①CG=CH;② GF=HF; ③FC平分分∠GCH;④FC平分∠GFH;一定正确的有 (填写序号,不要求证明)


查看答案和解析>>
科目:初中数学 来源: 题型:
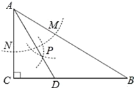
【题目】如图,在Rt△ABC中,∠C=90,∠B=30,以点A为圆心,任意长为半径画弧,分别交AB,AC于点M,N,再分别以点M,N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,
MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,
(1)判断下列命题的真假
①AD是△ABC的角平分线 ( )
②点D在AB的中垂线上 ( )
③S△ADC:S△ADB=1:2( )
(2)从(1)的②③两个命题中,选择一个真命题,写出证明。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AD∥BC,∠ABC+∠DCB=90°,且BC=2AD,以AB、BC、DC为边向外作正方形,其面积分别为S1、S2、S3,若S1=4,S3=12,则S2的值为( )

A.16B.24C.48D.64
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上的点,
上的点,![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() ,垂足分别是
,垂足分别是![]() ,
,![]() ,若
,若![]() ,
,![]() ,那么下面四个结论:①
,那么下面四个结论:①![]() ;②
;②![]() //
//![]() ;③△
;③△![]() ≌△
≌△![]() ;④
;④![]() ,其中一定正确的是(填写编号)_____________.
,其中一定正确的是(填写编号)_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx﹣2(a≠0)的图象的顶点在第三象限,且过点(1,0),设t=a﹣b﹣2,则t值的变化范围是( )
A. ﹣2<t<0 B. ﹣3<t<0 C. ﹣4<t<﹣2 D. ﹣4<t<0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com