
【题目】如图,四边形ABCD中,AD∥BC,∠ABC+∠DCB=90°,且BC=2AD,以AB、BC、DC为边向外作正方形,其面积分别为S1、S2、S3,若S1=4,S3=12,则S2的值为( )

A.16B.24C.48D.64
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,为了测量河对岸l1上两棵古树A、B之间的距离,某数学兴趣小组在河这边沿着与AB平行的直线l2上取C、D两点,测得∠ACB=15°,∠ACD=45°,若l1、l2之间的距离为50m,则A、B之间的距离为( )
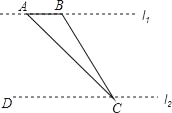
A. 50m B. 25m C. (50﹣![]() )m D. (50﹣25
)m D. (50﹣25![]() )m
)m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(1,2)且与x轴交点的横坐标分别为x1,x2,其中﹣1<x1<0.1<x2<2.下列结论:4a+2b+c<0;2a+b<0;b2+8a>4ac;
a<﹣1;其中结论正确的有( )
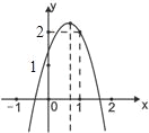
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.

(1)求证:△DEF是等腰三角形;
(2)当∠A=36°时,求∠DEF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是矩形ABCD的对角线AC的中点,E是AD的中点.若AB=6,AD=8,则四边形ABPE的周长为( )

A. 14 B. 16 C. 17 D. 18
查看答案和解析>>
科目:初中数学 来源: 题型:
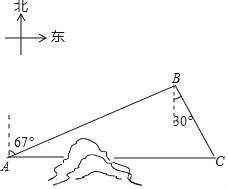
【题目】如图,C地在A地的正东方向,因有大山阻隔,由A地到C地需要绕行B地,已知B地位于A地北偏东67°方向,距离A地520km,C地位于B地南偏东30°方向,若打通穿山隧道,建成两地直达高铁,求A地到C地之间高铁线路的长(结果保留整数)
(参考数据:sin67°≈0.92;cos67°≈0.38;![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为平行四边形ABCD的边AD上的一点,E、F分别为PB、PC的中点,△PEF、△PDC、△PAB的面积分别为S、S1、S2.若S=3,则S1+S2的值为( )

A. 3 B. 6 C. 12 D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图与设计:
在图1和图2中,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.

(1)在图1中以格点为顶点画一个三角形,使三角形三边长分别为![]() ,
,![]() ,4;
,4;
(2)在图2中以格点为顶点画一个面积为10的正方形;
(3)在图3的正方形网格中建立平面直角坐标系,若![]() 各顶点的坐标分别为:
各顶点的坐标分别为:![]() ,
,![]() ,
,![]() ,请你作
,请你作![]() ,使
,使![]() 和
和![]() 关于
关于![]() 轴对称.
轴对称.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂计划生产A、B两种产品共50件.已知A产品每件可获利润1200元,B产品每件可获利润700元,设生产两种产品的获利总额为y(元),生产A产品x(件).
(1)写出y与x之间的函数关系式;
(2)若生产A、B两种产品的件数均不少于10件,求总利润的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com