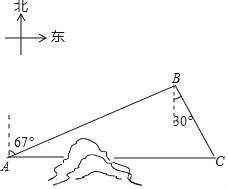
【题目】如图，C地在A地的正东方向，因有大山阻隔，由A地到C地需要绕行B地，已知B地位于A地北偏东67°方向，距离A地520km，C地位于B地南偏东30°方向，若打通穿山隧道，建成两地直达高铁，求A地到C地之间高铁线路的长（结果保留整数）
（参考数据：sin67°≈0.92；cos67°≈0.38；
≈1.73）
【答案】A地到C地之间高铁线路的长为592km．
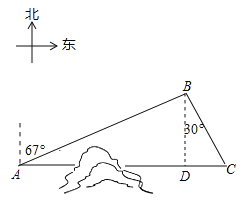
【解析】分析：过点B作BD⊥AC于点D，利用锐角三角函数的定义求出AD及CD的长，进而可得出结论．
详解：过点B作BD⊥AC于点D．
∵B地位于A地北偏东67°方向，距离A地520km，∴∠ABD=67°，
∴AD=ABsin67°=520×0.92=478.4km，BD=ABcos67°=520×0.38=197.6km．
∵C地位于B地南偏东30°方向，∴∠CBD=30°，
∴CD=BDtan30°=197.6×
≈113.9km，
∴AC=AD+CD=478.4+113.9≈592（km）．
答：A地到C地之间高铁线路的长为592km．
科目：初中数学 来源： 题型：
【题目】如图，点P是∠AOB内任意一点，且∠AOB＝40°，点M和点N分别是射线OA和射线OB上的动点，当△PMN周长取最小值时,则∠MPN的度数为（ ）
A. 140° B. 100° C. 50° D. 40°
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,在Rt△ABC中,∠C=90,∠B=30,以点A为圆心,任意长为半径画弧,分别交AB,AC于点M,N,再分别以点M,N为圆心,大于
MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,
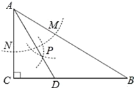
（1）判断下列命题的真假
①AD是△ABC的角平分线 ( )
②点D在AB的中垂线上 ( )
③S△ADC:S△ADB=1:2( )
（2）从（1）的②③两个命题中，选择一个真命题，写出证明。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，四边形ABCD中，AD∥BC，∠ABC+∠DCB＝90°，且BC＝2AD，以AB、BC、DC为边向外作正方形，其面积分别为S1、S2、S3，若S1＝4，S3＝12，则S2的值为（ ）
A.16B.24C.48D.64
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平行四边形ABCD中，AC⊥CD，将线段AD绕点D按逆时针方向旋转，旋转后交AC于点E，交BC于点F．
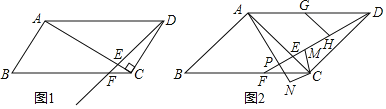
（1）若∠CAD＝30°，线段AD绕点D按逆时针方向旋转45°，且CE＝1，求AD；
（2）若∠CAD＝45°，线段AD绕点D按逆时针方向旋转30°，点M是线段DF上任意一点（M不与D重合），连接CM，将线段CM绕点C按逆时针方向旋转90°得到线段CN，连接AN交射线DE于点P，点G、H分别是AD、DE的中点，求证：CD＝CE+2CP．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△
中，
，
分别是
，
上的点，
⊥
，
⊥，垂足分别是
，
，若
，
，那么下面四个结论：①
；②
//
；③△
≌△
；④
，其中一定正确的是（填写编号）_____________.
查看答案和解析>>
科目：初中数学 来源： 题型：
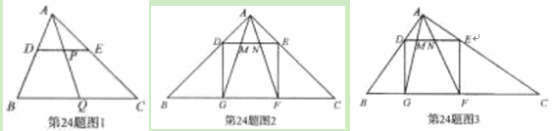
【题目】（本题满分10分）（1）如图1，在△ABC中，点D，E，Q分别在AB，AC，BC上，且DE∥BC，AQ交DE于点P.求证：
.
（2）如图，在△ABC中，∠BAC=90°，正方形DEFG的四个顶点在△ABC的边上，连接AG，AF分别交DE于M，N两点.
①如图2，若AB=AC=1，直接写出MN的长；
②如图3，求证MN2=DM·EN.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，某同学把一块三角形的玻璃打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的办法是（ ）
A.带①去B.带②去C.带③去D.带①和②去
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
