
【题目】如图,在平行四边形ABCD中,AC⊥CD,将线段AD绕点D按逆时针方向旋转,旋转后交AC于点E,交BC于点F.
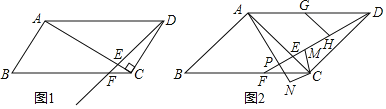
(1)若∠CAD=30°,线段AD绕点D按逆时针方向旋转45°,且CE=1,求AD;
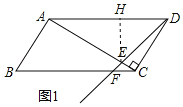
(2)若∠CAD=45°,线段AD绕点D按逆时针方向旋转30°,点M是线段DF上任意一点(M不与D重合),连接CM,将线段CM绕点C按逆时针方向旋转90°得到线段CN,连接AN交射线DE于点P,点G、H分别是AD、DE的中点,求证:CD=CE+2CP.
【答案】(1)AD=4+2![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)由直角三角形的性质可求AD=(![]() +1)HE,CD=
+1)HE,CD=![]() HE,AC=
HE,AC=![]() HE,由CE=AC﹣AE=1,可求AD的长;
HE,由CE=AC﹣AE=1,可求AD的长;
(2)如图2,连接CH,CP,MN,通过证明∴△ACN≌△DCM,△DGH≌△HPC,可得∠CDM=∠CAN=15°,GH=PC,即可求解.
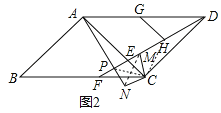
解:(1)过点E作EH⊥AD,
∵线段AD绕点D按逆时针方向旋转45°,
∴∠ADE=45°,且EH⊥AD,
∴∠HED=∠HDE=45°,
∴HE=HD,
∵∠DAC=30°,HE⊥AD,∠ACD=90°,
∴AH=![]() HE,AE=2HE,AD=2CD,AC=
HE,AE=2HE,AD=2CD,AC=![]() CD,
CD,
∴AD=(![]() +1)HE,
+1)HE,
∴CD=![]() HE,AC=
HE,AC=![]() HE,
HE,
∵CE=AC﹣AE=(![]() ﹣2)HE=1
﹣2)HE=1
∴HE=![]() +1,
+1,
∴AD=(![]() )2=4+2
)2=4+2![]()
(2)如图2,连接CH,CP,MN,
∵线段AD绕点D按逆时针方向旋转30°,
∴∠ADH=30°
∵∠CAD=45°,AC⊥CD,
∴∠CAD=∠ADC=45°,
∴AC=CD,∠CDH=15°,
∵将线段CM绕点C按逆时针方向旋转90°得到线段CN,
∴CM=CN,∠MCN=∠ACD=90°,
∴∠MNC=∠NMC=45°,∠MCN﹣∠ACM=∠ACD﹣∠ACM,
∴∠ACN=∠DCM,且AC=CD,CN=CM,
∴△ACN≌△DCM(SAS)
∴∠CDM=∠CAN=15°,
∴∠APD=180°﹣∠ADE﹣∠CAD﹣∠CAN=180°﹣30°﹣45°﹣15°=90°,
∴∠MPN=∠MCN=90°,
∴点M,点C,点N,点P四点共圆,
∴∠MPC=∠MNC=45°,
∵点 G,点H分别是AD,DE的中点,
∴AE=2GH,AE∥GH,
∴∠DGH=∠DAC=45°,
∵∠ACD=90°,点H是DE中点,
∴CH=DH=EH,
∴∠HCD=∠HDC=15°,
∴∠PHC=30°,
∴∠PHC=∠GDH=30°,且CH=DH,∠DGH=∠HPC=45°,
∴△DGH≌△HPC(AAS)
∴GH=PC,
∴AE=2GH=2PC,
∴CD=AC=AE+CE=CE+2CP.


科目:初中数学 来源: 题型:
【题目】如图,点![]() 是等边三角形
是等边三角形![]() 内一点,
内一点,![]() 将
将![]() 绕点
绕点![]() .按顺时针方向旋转
.按顺时针方向旋转![]() 得
得![]() , 连接
, 连接![]() .
.
(1)求证:![]() 是等边三角形;
是等边三角形;
(2)当![]() 时, 试判断
时, 试判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)探究:当![]() 为多少度时,
为多少度时,![]() 是等腰三角形.
是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
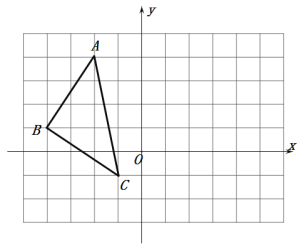
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,4),B(-4,1),C(-1,-1)
(1)直接写出△ABC的面积;
(2)在图中作出△ABC关于x轴的对称△A1B1C1;
(3)将△ABC向右平移5个单位,向上平移一个单位,得到△A2B2C2,并写出B2的坐标;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“品中华诗词,寻文化基因”.某校举办了第二届“中华诗词大赛”,将该校八年级参加竞赛的学生成绩统计后,绘制了如下不完整的频数分布统计表与频数分布直方图.
频数分布统计表
组别 | 成绩x(分) | 人数 | 百分比 |
A | 60≤x<70 | 8 | 20% |
B | 70≤x<80 | 16 | m% |
C | 80≤x<90 | a | 30% |
D | 90≤<x≤100 | 4 | 10% |
请观察图表,解答下列问题:
(1)表中a= ,m= ;
(2)补全频数分布直方图;
(3)D组的4名学生中,有1名男生和3名女生.现从中随机抽取2名学生参加市级竞赛,则抽取的2名学生恰好是一名男生和一名女生的概率为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
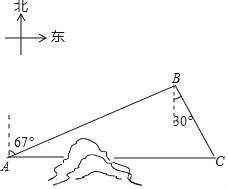
【题目】如图,C地在A地的正东方向,因有大山阻隔,由A地到C地需要绕行B地,已知B地位于A地北偏东67°方向,距离A地520km,C地位于B地南偏东30°方向,若打通穿山隧道,建成两地直达高铁,求A地到C地之间高铁线路的长(结果保留整数)
(参考数据:sin67°≈0.92;cos67°≈0.38;![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
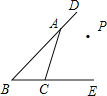
【题目】如图,已知点P到BE,BD,AC的距离恰好相等,则点P的位置:①在∠B的平分线上;②在∠DAC的平分线上;③在∠ECA的平分线上;④恰是∠B,∠DAC,∠ECA三条角平分线的交点,上述结论中,正确结论的个数有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,某校数学兴趣小组为测得大厦AB的高度,在大厦前的平地上选择一点C,测得大厦顶端A的仰角为30°,再向大厦方向前进80米,到达点D处(C、D、B三点在同一直线上),又测得大厦顶端A的仰角为45°,请你计算该大厦的高度.(精确到0.1米,参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ACB和△ECD都是等腰直角三角形,A、C、D三点在同一直线上,连接BD、AE,并延长AE交BD于F.
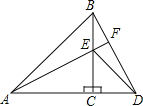
(1)求证:AE=BD;
(2)试判断直线AE与BD的位置关系,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com