【题目】如图，已知点P到BE，BD，AC的距离恰好相等，则点P的位置：①在∠B的平分线上；②在∠DAC的平分线上；③在∠ECA的平分线上；④恰是∠B，∠DAC，∠ECA三条角平分线的交点，上述结论中，正确结论的个数有（ ）
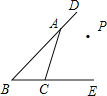
A.1个B.2个C.3个D.4个
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】在“朗读者”节目的影响下，某中学开展了“好书伴我成长”的读书活动，为了解3月份七年级300名学生读书情况，随机调查了七年级50个学生读书的册数，统计数据如下表所示：
册数 | 0 | 1 | 2 | 3 | 4 |
人数 | 4 | 12 | 16 | 17 | 1 |
关于这组数据，下列说法正确的是（ ）
A. 众数是 17 B. 平均数是 2 C. 中位数是 2 D. 方差是 2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校计划组织师生共310人参加一次野外研学活动,如果租用6辆大客车和5辆小客车恰好全部坐满.已知每辆大客车的乘客座位数比小客车多15个.
（1）求每辆大客车和每辆小客车的乘客座位数；
（2）由于最后参加活动的人数增加了20人,学校决定调整租车方案,在保持租用车辆总数不变的情况下,为将所有参加活动的师生装载完成,求租用小客车数量的最大值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平行四边形ABCD中，AC⊥CD，将线段AD绕点D按逆时针方向旋转，旋转后交AC于点E，交BC于点F．
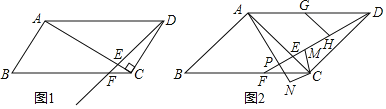
（1）若∠CAD＝30°，线段AD绕点D按逆时针方向旋转45°，且CE＝1，求AD；
（2）若∠CAD＝45°，线段AD绕点D按逆时针方向旋转30°，点M是线段DF上任意一点（M不与D重合），连接CM，将线段CM绕点C按逆时针方向旋转90°得到线段CN，连接AN交射线DE于点P，点G、H分别是AD、DE的中点，求证：CD＝CE+2CP．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，在ABCD中，E是CD延长线上的一点，BE与AD交于点F，DE＝
CD.
(1)求证：△ABF∽△CEB；
(2)若△DEF的面积为2，求ABCD的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
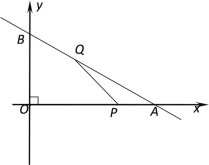
【题目】如图，已知直线l的函数表达式为y=
x+6，且l与x轴、y轴分别交于A、B两点，动点Q从B点开始在线段BA上以每秒2个单位的速度向点A移动，同时动点P从A点开始在线段AO上以每秒1个单位的速度向O点移动，设点Q、P移动时间为t秒．
（1）求点A、B的坐标
（2）当以点A、P、Q为顶点的三角形是等腰三角形时,求时间t的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】观察下列方程及其解的特征：
（1）
的解为
；
（2）
的解为
，
；
（3）
的解为
，
；
解答下列问题：
请猜想：方程
的解为________；
请猜想：关于
的方程
________的解为
，
；
下面以解方程为例，验证中猜想结论的正确性．
解：原方程可化为
．
（下面请大家用配方法写出解此方程的详细过程）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线MN经过正方形ABCD的顶点D且不与正方形的任何一边相交，AM⊥MN于M，CN⊥MN于N，BR⊥MN于R。
(1)求证：△ADM≌△DCN
(2)求证：MN=AM+CN
(3)试猜想BR与MN的数量关系，并证明你的猜想
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
