
【题目】已知A(﹣2,3),B(1,![]() ),点P为x轴上一点,使得△PAB的面积等于
),点P为x轴上一点,使得△PAB的面积等于![]() ,则点P的坐标为_____.
,则点P的坐标为_____.
【答案】(﹣![]() ,0)或(
,0)或(![]() ,0)
,0)
【解析】
如图,设直线AB的解析式为y=kx+b,求得直线AB的解析式为y=﹣![]() x+2,当y=0时,x=4,得到点C的坐标为(4,0),设点P的坐标为(a,0),则PC=|4﹣a|,根据三角形的面积公式即可得到结论.
x+2,当y=0时,x=4,得到点C的坐标为(4,0),设点P的坐标为(a,0),则PC=|4﹣a|,根据三角形的面积公式即可得到结论.
解:如图,设直线AB的解析式为y=kx+b,

∵A(﹣2,3),B(1,![]() ),
),
∴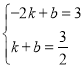 ,
,
解得: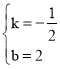 ,
,
∴直线AB的解析式为y=﹣![]() x+2,
x+2,
当y=0时,x=4,
∴点C的坐标为(4,0),
设点P的坐标为(a,0),则PC=|4﹣a|,
依据S△PAB=S△PAC﹣S△PBC可得,
![]() =
=![]() ×PC×3﹣
×PC×3﹣![]() ×PC×
×PC×![]() ,即
,即![]() =
=![]() |4﹣a|×
|4﹣a|×![]() ,
,
解得a=﹣![]() 或
或![]() ,
,
∴点P的坐标为(﹣![]() ,0)或(
,0)或(![]() ,0),
,0),
故答案为:(﹣![]() ,0)或(
,0)或(![]() ,0).
,0).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
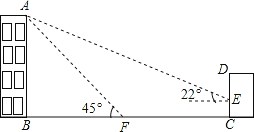
【题目】如图,宿豫区某校教学楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,教学楼在建筑物的墙上留下高3米的影子CE,而当光线与地面夹角是45°时,教学楼顶A在地面上的影子F与墙角C有30米的距离(B、F、C在一条直线上).
(1)求教学楼AB的高度;
(2)若要在A、E之间挂一些彩旗,请你求出A、E之间的距离.(结果精确到lm)(参考数据:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图像与x轴和y轴分别交于点A和B,再将
的图像与x轴和y轴分别交于点A和B,再将![]() 沿直线CD对折,使点A与点B重合,直线CD与x轴交于点C,与AB交于点D,连接BC.
沿直线CD对折,使点A与点B重合,直线CD与x轴交于点C,与AB交于点D,连接BC.
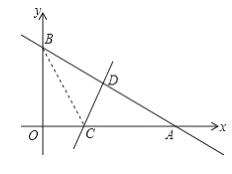
(1)求点A和点B的坐标;
(2)求![]() ;
;
(3)在y轴上有一点P,且![]() 是等腰三角形,求出点P的坐标.
是等腰三角形,求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,△ABC是等边三角形,过点C作CD∥AB,且CD=AB,连接BD交AC于点O.
(1)如图1,求证:AC垂直平分BD;
(2)如图2,点M在BC的延长线上,点N在线段CO上,且ND=NM,连接BN.求证:NB=NM.
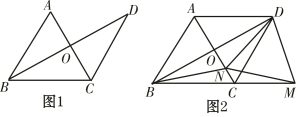
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“品中华诗词,寻文化基因”.某校举办了第二届“中华诗词大赛”,将该校八年级参加竞赛的学生成绩统计后,绘制了如下不完整的频数分布统计表与频数分布直方图.
频数分布统计表
组别 | 成绩x(分) | 人数 | 百分比 |
A | 60≤x<70 | 8 | 20% |
B | 70≤x<80 | 16 | m% |
C | 80≤x<90 | a | 30% |
D | 90≤<x≤100 | 4 | 10% |
请观察图表,解答下列问题:
(1)表中a= ,m= ;
(2)补全频数分布直方图;
(3)D组的4名学生中,有1名男生和3名女生.现从中随机抽取2名学生参加市级竞赛,则抽取的2名学生恰好是一名男生和一名女生的概率为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l1:y1=![]() x+3经过点A(m,5),与y轴的交点为B;直线l2:y2=kx+b经过点A和C(2,﹣1).
x+3经过点A(m,5),与y轴的交点为B;直线l2:y2=kx+b经过点A和C(2,﹣1).
(1)求直线l2的解析式,并直接写出不等式y1≥y2的解集;
(2)求△AOB的面积.
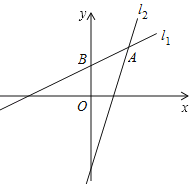
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点P到BE,BD,AC的距离恰好相等,则点P的位置:①在∠B的平分线上;②在∠DAC的平分线上;③在∠ECA的平分线上;④恰是∠B,∠DAC,∠ECA三条角平分线的交点,上述结论中,正确结论的个数有( )
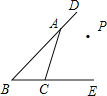
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图形的折叠即图形的翻折或者说是对称变换.这类问题与生活紧密联系,内容丰富,解法灵活,具有开放性,可以培养我们的动手能力,空间想象能力和几何变换的思想.在综合与实践课上,每个小组剪了一些如图1所示的直角三角形纸片(![]() ,
,![]() ,
,![]() ),并将
),并将![]() 纸片中的各内角进行折叠操作:
纸片中的各内角进行折叠操作:
(1)如图2,“奋斗”小组将![]() 纸片中的
纸片中的![]() 进行折叠,使直角边
进行折叠,使直角边![]() 落在斜边
落在斜边![]() 上,点
上,点![]() 落在点
落在点![]() 位置,折痕为
位置,折痕为![]() ,则
,则![]() 的长为______
的长为______![]() .
.

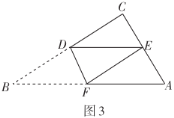
(2)如图3,“勤奋”小组将![]() 中的
中的![]() 进行折叠,使点
进行折叠,使点![]() 落在直角边
落在直角边![]() 中点
中点![]() 上,折痕为
上,折痕为![]() ,则
,则![]() 的长为______
的长为______![]() .
.
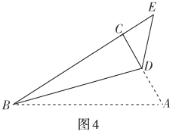
(3)如图4,“雄鹰”小组将![]() 纸片中的
纸片中的![]() 进行折叠,使点
进行折叠,使点![]() 落在直角边
落在直角边![]() 延长线上的点
延长线上的点![]() 处,折痕为
处,折痕为![]() ,求出
,求出![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】打折前,买20件A商品和30件B商品要用2200元,买50件A商品和10件B商品要用2900元.若打折后,买40件A商品和40件B商品用了3240元,比不打折少花多少钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com