
【题目】如图,一次函数![]() 的图像与x轴和y轴分别交于点A和B,再将
的图像与x轴和y轴分别交于点A和B,再将![]() 沿直线CD对折,使点A与点B重合,直线CD与x轴交于点C,与AB交于点D,连接BC.
沿直线CD对折,使点A与点B重合,直线CD与x轴交于点C,与AB交于点D,连接BC.
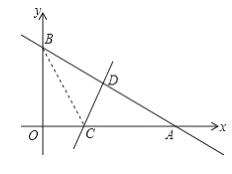
(1)求点A和点B的坐标;
(2)求![]() ;
;
(3)在y轴上有一点P,且![]() 是等腰三角形,求出点P的坐标.
是等腰三角形,求出点P的坐标.
【答案】(1)A的坐标为(4,0) B的坐标为(0,3)(2)![]() (3)(0,8)、(0,-2)、(0,-3)、(0,
(3)(0,8)、(0,-2)、(0,-3)、(0,![]() ).
).
【解析】
(1)令y=0求出x的值,再令x=0求出y的值,即可求出A、B两点的坐标.(2)根据勾股定理求出OC的长即可解决.(3)在y轴上有一点P,且△PAB是等腰三角形,分三种情况讨论,即当BP=BA时;当AP=AB时;当PB=PA时.
解:⑴因为A、B两点都在一次函数![]() 的直线上
的直线上
令y = 0则x = 4;令x = 0,则y = 3,
故点A的坐标为(4,0),点B的坐标为(0,3).
(2)设 OC =m,则 AC=CB =4-m
∵∠BOA = 90°,
∴![]() ,
,
![]() ,
,
解得![]() .
.
∴![]() ,
,
![]()
(3)∵A的坐标为(4,0),B的坐标为(0,3)
∴OB=3,OA=4,在Rt△OAB中
![]()
所以AB=5
当BP=BA时,P点可能在B点上方,也可能在B点下方,
当P点可能在B点上方时,OP=OB+BP=3+5=8,此时P点坐标为(0,8)
当P点可能在B点下方时,OP=BP-OB=5-3=2,此时P点坐标为(0,-2)
当AP=AB时,x轴为三角形ABP的垂直平分线,此时OB=OP,此时P点坐标为(0,-3)
当PB=PA时,设P点坐标为(0,n),![]()
整理得:6n+7=0,解得n=![]() ,故P点坐标为(0,
,故P点坐标为(0,![]() )
)
故点P的坐标为:0,8)、(0,-2)、(0,-3)、(0,![]() ).
).


科目:初中数学 来源: 题型:
【题目】在“朗读者”节目的影响下,某中学开展了“好书伴我成长”的读书活动,为了解3月份七年级300名学生读书情况,随机调查了七年级50个学生读书的册数,统计数据如下表所示:
册数 | 0 | 1 | 2 | 3 | 4 |
人数 | 4 | 12 | 16 | 17 | 1 |
关于这组数据,下列说法正确的是( )
A. 众数是 17 B. 平均数是 2 C. 中位数是 2 D. 方差是 2
查看答案和解析>>
科目:初中数学 来源: 题型:
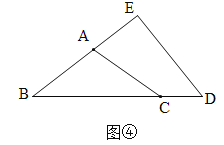
【题目】已知:在△ABC中,AB=AC.D是直线BC上的点,DE⊥AB.垂足是点E.
(1)如图①,当∠A=50![]() ,点D在线段BC延长线上时,∠EOB=____;
,点D在线段BC延长线上时,∠EOB=____;
(2)如图②,当∠A=50![]() ,点D在线段BC上时,∠EDB=____;
,点D在线段BC上时,∠EDB=____;
(3)如图③,当∠A=110![]() ,点D在线段BC上时,∠EDB=____;
,点D在线段BC上时,∠EDB=____;

(4)结合(1)、(2)、(3)的结果可以发现,∠EDB与∠A的数量关系是∠EDB=____∠A.
(5)按你发现的规律,当点D在线段BC延长线上,∠EDB=50![]() ,其余条件不变时如图④,不用计算,直接填空∠BAC=____.
,其余条件不变时如图④,不用计算,直接填空∠BAC=____.
查看答案和解析>>
科目:初中数学 来源: 题型:
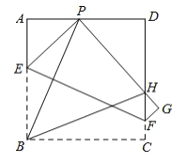
【题目】如图,现有一张边长为![]() 的正方形ABCD,点P 为正方形 AD 边上的一点(不与点 A、点D 重合),将正方形纸片折叠,使点 B 落在 P 处,点 C 落在 G 处,PG 交DC 于H,折痕为 EF,连接 BP,BH.
的正方形ABCD,点P 为正方形 AD 边上的一点(不与点 A、点D 重合),将正方形纸片折叠,使点 B 落在 P 处,点 C 落在 G 处,PG 交DC 于H,折痕为 EF,连接 BP,BH.
(1)求证:![]() ;
;
(2)求证:![]() ;
;
(3)当点P在边AD上移动时,△PDH的周长是否发生变化?不变化,求出周长,若变化,说明理由;
(4)设AP为x,四边形EFGP的面积为S,求出S与x的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面角坐标系中,函数y=2x和y=-x的图像分别为直线l1、l2,过点(1,0)作x轴的垂线交l2于点A1,过点A1作y轴的垂线交l2于点A2,过点A2作x轴的垂线交l1于点A3,过点A3作y轴的垂线交l2于点A4,…,依次进行下去,则点A2020的坐标为_______________
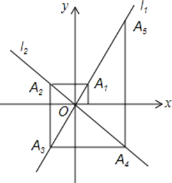
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划组织师生共310人参加一次野外研学活动,如果租用6辆大客车和5辆小客车恰好全部坐满.已知每辆大客车的乘客座位数比小客车多15个.
(1)求每辆大客车和每辆小客车的乘客座位数;
(2)由于最后参加活动的人数增加了20人,学校决定调整租车方案,在保持租用车辆总数不变的情况下,为将所有参加活动的师生装载完成,求租用小客车数量的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列方程及其解的特征:
(1)![]() 的解为
的解为![]() ;
;
(2)![]() 的解为
的解为![]() ,
,![]() ;
;
(3)![]() 的解为
的解为![]() ,
,![]() ;
;
解答下列问题:
![]() 请猜想:方程
请猜想:方程![]() 的解为________;
的解为________;
![]() 请猜想:关于
请猜想:关于![]() 的方程
的方程![]() ________的解为
________的解为![]() ,
,![]() ;
;
![]() 下面以解方程
下面以解方程![]() 为例,验证
为例,验证![]() 中猜想结论的正确性.
中猜想结论的正确性.
解:原方程可化为![]() .
.
(下面请大家用配方法写出解此方程的详细过程)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com