
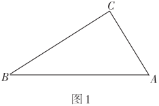
【题目】图形的折叠即图形的翻折或者说是对称变换.这类问题与生活紧密联系,内容丰富,解法灵活,具有开放性,可以培养我们的动手能力,空间想象能力和几何变换的思想.在综合与实践课上,每个小组剪了一些如图1所示的直角三角形纸片(![]() ,
,![]() ,
,![]() ),并将
),并将![]() 纸片中的各内角进行折叠操作:
纸片中的各内角进行折叠操作:
(1)如图2,“奋斗”小组将![]() 纸片中的
纸片中的![]() 进行折叠,使直角边
进行折叠,使直角边![]() 落在斜边
落在斜边![]() 上,点
上,点![]() 落在点
落在点![]() 位置,折痕为
位置,折痕为![]() ,则
,则![]() 的长为______
的长为______![]() .
.

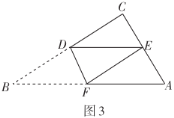
(2)如图3,“勤奋”小组将![]() 中的
中的![]() 进行折叠,使点
进行折叠,使点![]() 落在直角边
落在直角边![]() 中点
中点![]() 上,折痕为
上,折痕为![]() ,则
,则![]() 的长为______
的长为______![]() .
.
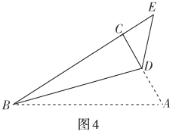
(3)如图4,“雄鹰”小组将![]() 纸片中的
纸片中的![]() 进行折叠,使点
进行折叠,使点![]() 落在直角边
落在直角边![]() 延长线上的点
延长线上的点![]() 处,折痕为
处,折痕为![]() ,求出
,求出![]() 的长.
的长.
【答案】(1)3;(2)![]() ;(3)
;(3)![]() 长为
长为![]() .
.
【解析】
(1)设CD为xcm,则BD=BC-CD=(8-x)cm,利用折叠的性质表示出DE、BE,在Rt△BDE中,利用勾股定理得![]() ,得到一个关于x的方程,解出即可.
,得到一个关于x的方程,解出即可.
(2)设BD为ycm,则CD=BC-BD=(8-y)cm. 利用折叠的性质表示出DE、CE、DE,在Rt△CDE中,![]() ,得到一个关于y的方程,解出即可.
,得到一个关于y的方程,解出即可.
(3)在![]() 中,利用勾股定理求AB,进而利用折叠的性质求BE,CE,设
中,利用勾股定理求AB,进而利用折叠的性质求BE,CE,设![]() ,则
,则![]() ,
,![]() ,在
,在![]() 中,根据勾股定理得
中,根据勾股定理得![]() ,
,
可得![]() ,解出即可.
,解出即可.
解:(1)设CD为xcm,则BD=BC-CD=(8-x)cm.
∵![]() 纸片中的
纸片中的![]() 进行折叠,使直角边
进行折叠,使直角边![]() 落在斜边
落在斜边![]() 上,点
上,点![]() 落在点
落在点![]() 位置
位置
∴DE=CD=xcm,AE=AC=6cm,BE=AB-AE=10-6=4cm
∴在Rt△BDE中,利用勾股定理得![]()
![]()
解得x=3cm
(2)设BD为ycm,则CD=BC-BD=(8-y)cm.
∵![]() 中的
中的![]() 进行折叠,使点
进行折叠,使点![]() 落在直角边
落在直角边![]() 中点
中点![]() 上,折痕为
上,折痕为![]()
∴DE=BD=ycm,CE=![]() =6cm
=6cm
∴在Rt△CDE中,利用勾股定理得![]()
![]()
解得y=![]() cm
cm
(3)在![]() 中,
中,
![]() ,
,
根据折叠的性质可知:![]() ,
,
∵![]() ,
,
∴![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,
在![]() 中,根据勾股定理得
中,根据勾股定理得
![]() ,
,
即![]() ,
,
解得![]() ,
,
即![]() 长为
长为![]() .
.


科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,AB=AC.D是直线BC上的点,DE⊥AB.垂足是点E.
(1)如图①,当∠A=50![]() ,点D在线段BC延长线上时,∠EOB=____;
,点D在线段BC延长线上时,∠EOB=____;
(2)如图②,当∠A=50![]() ,点D在线段BC上时,∠EDB=____;
,点D在线段BC上时,∠EDB=____;
(3)如图③,当∠A=110![]() ,点D在线段BC上时,∠EDB=____;
,点D在线段BC上时,∠EDB=____;

(4)结合(1)、(2)、(3)的结果可以发现,∠EDB与∠A的数量关系是∠EDB=____∠A.
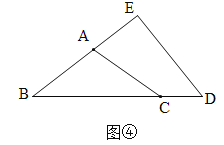
(5)按你发现的规律,当点D在线段BC延长线上,∠EDB=50![]() ,其余条件不变时如图④,不用计算,直接填空∠BAC=____.
,其余条件不变时如图④,不用计算,直接填空∠BAC=____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在ABCD中,E是CD延长线上的一点,BE与AD交于点F,DE=![]() CD.
CD.
(1)求证:△ABF∽△CEB;
(2)若△DEF的面积为2,求ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
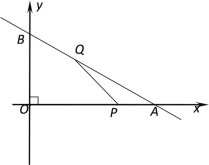
【题目】如图,已知直线l的函数表达式为y=![]() x+6,且l与x轴、y轴分别交于A、B两点,动点Q从B点开始在线段BA上以每秒2个单位的速度向点A移动,同时动点P从A点开始在线段AO上以每秒1个单位的速度向O点移动,设点Q、P移动时间为t秒.
x+6,且l与x轴、y轴分别交于A、B两点,动点Q从B点开始在线段BA上以每秒2个单位的速度向点A移动,同时动点P从A点开始在线段AO上以每秒1个单位的速度向O点移动,设点Q、P移动时间为t秒.
(1)求点A、B的坐标
(2)当以点A、P、Q为顶点的三角形是等腰三角形时,求时间t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列方程及其解的特征:
(1)![]() 的解为
的解为![]() ;
;
(2)![]() 的解为
的解为![]() ,
,![]() ;
;
(3)![]() 的解为
的解为![]() ,
,![]() ;
;
解答下列问题:
![]() 请猜想:方程
请猜想:方程![]() 的解为________;
的解为________;
![]() 请猜想:关于
请猜想:关于![]() 的方程
的方程![]() ________的解为
________的解为![]() ,
,![]() ;
;
![]() 下面以解方程
下面以解方程![]() 为例,验证
为例,验证![]() 中猜想结论的正确性.
中猜想结论的正确性.
解:原方程可化为![]() .
.
(下面请大家用配方法写出解此方程的详细过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王华、张伟两位同学分别将自己10次数学自我检测的成绩绘制成如下统计图:

(1)根据图中提供的数据列出如下统计表:
平均成绩(分) | 中位数(分) | 众数(分) | 方差(S2) | |
王华 | 80 | b | 80 | d |
张伟 | a | 85 | c | 260 |
则a= ,b= ,c= ,d= ,
(2)将90分以上(含90分)的成绩视为优秀,则优秀率高的是 .
(3)现在要从这两个同学选一位去参加数学竞赛,你可以根据以上的数据给老师哪些建议?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,AB∶BC∶CA=3∶4∶5,且周长为36 cm,点P从点A开始沿AB边向B点以每秒1cm的速度移动;点Q从点B沿BC边向点C以每秒2cm的速度移动,如果同时出发,则过3s时,△BPQ的面积为____cm2.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com