
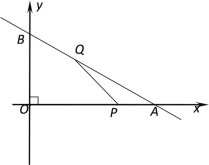
【题目】如图,已知直线l的函数表达式为y=![]() x+6,且l与x轴、y轴分别交于A、B两点,动点Q从B点开始在线段BA上以每秒2个单位的速度向点A移动,同时动点P从A点开始在线段AO上以每秒1个单位的速度向O点移动,设点Q、P移动时间为t秒.
x+6,且l与x轴、y轴分别交于A、B两点,动点Q从B点开始在线段BA上以每秒2个单位的速度向点A移动,同时动点P从A点开始在线段AO上以每秒1个单位的速度向O点移动,设点Q、P移动时间为t秒.
(1)求点A、B的坐标
(2)当以点A、P、Q为顶点的三角形是等腰三角形时,求时间t的值.
【答案】(1)A(8,0) B(0,6);(2)![]() ,
,![]() ,
,![]()
【解析】
(1)根据自变量与函数值的对应关系,可得相应的函数值,相应自变量的值;
(2)根据相似三角形的性质,可得关于t的方程,根据解方程,可得答案.
(1)∵直线的表达式为y=![]() x+6,
x+6,
令x=0,得y=6,
∴B(0,6),
令y=0,得0=![]() x+6,
x+6,
∴x=8,
∴ A(8,0) ;
(2)∵∠BOA=90°,
BO=6,AO=8,
∴AC=10,
由题意可知BQ=2t,AQ=10-2t,AP=t,
①当AQ=AP时,10-2t=t,
∴![]() ;
;
②当PQ=AP时,
过点P作PH⊥AQ,

∵PH⊥AQ,
∴∠PHA=∠AOB=90°,
∵∠HAP=∠OAB,
∴△AHP∽△AOB,
∴![]() ,
,
∵PQ=PA,PH⊥AQ,
∴AH=HQ,
∴AH=5-t,
∴![]() ,
,
∴![]() ;
;
③当QP=QA时,
过点Q作QH⊥AP,
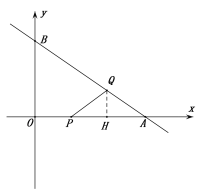
∵QH⊥AP,
∴∠QHA=∠AOB=90°,
∵∠QAH=∠BAO,
∴△AQH∽△ABO,
∴![]() ,
,
∵QP=QA,QH⊥AP,
∴AH=PH,
∴AH=![]() ,
,
∴![]() ,
,
∴![]() ,
,
综上所述当![]() ,
,![]() ,
,![]() 时,以点A、P、Q为顶点的三角形是等腰三角形.
时,以点A、P、Q为顶点的三角形是等腰三角形.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
【题目】如图所示,A、B两地之间有一条河,原来从A地到B地需要经过桥DC,沿折线A→D→C→B到达,现在新建了桥EF(EF=DC),可直接沿直线AB从A地到达B地,已知BC=12km,∠A=45°,∠B=30°,桥DC和AB平行.
(1)求桥DC与直线AB的距离;
(2)现在从A地到达B地可比原来少走多少路程?
(以上两问中的结果均精确到0.1km,参考数据:![]() ≈1.14,
≈1.14,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“品中华诗词,寻文化基因”.某校举办了第二届“中华诗词大赛”,将该校八年级参加竞赛的学生成绩统计后,绘制了如下不完整的频数分布统计表与频数分布直方图.
频数分布统计表
组别 | 成绩x(分) | 人数 | 百分比 |
A | 60≤x<70 | 8 | 20% |
B | 70≤x<80 | 16 | m% |
C | 80≤x<90 | a | 30% |
D | 90≤<x≤100 | 4 | 10% |
请观察图表,解答下列问题:
(1)表中a= ,m= ;
(2)补全频数分布直方图;
(3)D组的4名学生中,有1名男生和3名女生.现从中随机抽取2名学生参加市级竞赛,则抽取的2名学生恰好是一名男生和一名女生的概率为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点P到BE,BD,AC的距离恰好相等,则点P的位置:①在∠B的平分线上;②在∠DAC的平分线上;③在∠ECA的平分线上;④恰是∠B,∠DAC,∠ECA三条角平分线的交点,上述结论中,正确结论的个数有( )
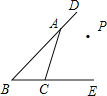
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,某校数学兴趣小组为测得大厦AB的高度,在大厦前的平地上选择一点C,测得大厦顶端A的仰角为30°,再向大厦方向前进80米,到达点D处(C、D、B三点在同一直线上),又测得大厦顶端A的仰角为45°,请你计算该大厦的高度.(精确到0.1米,参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
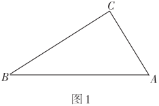
【题目】图形的折叠即图形的翻折或者说是对称变换.这类问题与生活紧密联系,内容丰富,解法灵活,具有开放性,可以培养我们的动手能力,空间想象能力和几何变换的思想.在综合与实践课上,每个小组剪了一些如图1所示的直角三角形纸片(![]() ,
,![]() ,
,![]() ),并将
),并将![]() 纸片中的各内角进行折叠操作:
纸片中的各内角进行折叠操作:
(1)如图2,“奋斗”小组将![]() 纸片中的
纸片中的![]() 进行折叠,使直角边
进行折叠,使直角边![]() 落在斜边
落在斜边![]() 上,点
上,点![]() 落在点
落在点![]() 位置,折痕为
位置,折痕为![]() ,则
,则![]() 的长为______
的长为______![]() .
.

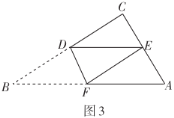
(2)如图3,“勤奋”小组将![]() 中的
中的![]() 进行折叠,使点
进行折叠,使点![]() 落在直角边
落在直角边![]() 中点
中点![]() 上,折痕为
上,折痕为![]() ,则
,则![]() 的长为______
的长为______![]() .
.
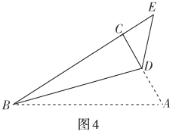
(3)如图4,“雄鹰”小组将![]() 纸片中的
纸片中的![]() 进行折叠,使点
进行折叠,使点![]() 落在直角边
落在直角边![]() 延长线上的点
延长线上的点![]() 处,折痕为
处,折痕为![]() ,求出
,求出![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.
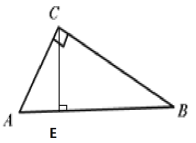
(1)根据已知条件,用尺规作图将图形补充完整,并保留作图痕迹。
(2)求证:△ACD≌△AED;
(3)若∠B=30°,CD=1,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l1:y=2x+3与x轴、y轴的交点分别为A、B两点,将直线l1向下平移1个长度单位后得到直线l2,直线l2与x轴交于点C,与y轴交于点D,
(1)求△AOB 的面积;
(2)直线l2的表达式;
(3)求△CBD的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com