
【题目】如图所示,在ABCD中,E是CD延长线上的一点,BE与AD交于点F,DE=![]() CD.
CD.
(1)求证:△ABF∽△CEB;
(2)若△DEF的面积为2,求ABCD的面积.

【答案】(1)见解析;(2)16
【解析】
试题(1)要证△ABF∽△CEB,需找出两组对应角相等;已知了平行四边形的对角相等,再利用AB∥CD,可得一对内错角相等,则可证.
(2)由于△DEF∽△EBC,可根据两三角形的相似比,求出△EBC的面积,也就求出了四边形BCDF的面积.同理可根据△DEF∽△AFB,求出△AFB的面积.由此可求出ABCD的面积.
试题解析:(1)证明:∵四边形ABCD是平行四边形
∴∠A=∠C,AB∥CD
∴∠ABF=∠CEB
∴△ABF∽△CEB
(2)解:∵四边形ABCD是平行四边形
∴AD∥BC,AB平行且等于CD
∴△DEF∽△CEB,△DEF∽△ABF
∵DE=![]() CD
CD
∴![]() ,
,
![]()
∵S△DEF=2
S△CEB=18,S△ABF=8,
∴S四边形BCDF=S△BCE-S△DEF=16
∴S四边形ABCD=S四边形BCDF+S△ABF=16+8=24.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:初中数学 来源: 题型:
【题目】如图,有6个质地和大小均相同的球,每个球只标有一个数字,将标有3,4,5的三个球放入甲箱中,标有4,5,6的三个球放入乙箱中.
(1)小宇从甲箱中随机模出一个球,求“摸出标有数字是3的球”的概率;
(2)小宇从甲箱中、小静从乙箱中各自随机摸出一个球,若小宇所摸球上的数字比小静所摸球上的数字大1,则称小宇“略胜一筹”.请你用列表法(或画树状图)求小宇“略胜一筹”的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
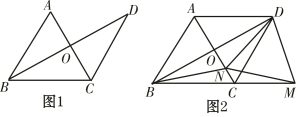
【题目】已知,△ABC是等边三角形,过点C作CD∥AB,且CD=AB,连接BD交AC于点O.
(1)如图1,求证:AC垂直平分BD;
(2)如图2,点M在BC的延长线上,点N在线段CO上,且ND=NM,连接BN.求证:NB=NM.
查看答案和解析>>
科目:初中数学 来源: 题型:
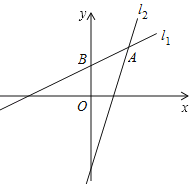
【题目】已知直线l1:y1=![]() x+3经过点A(m,5),与y轴的交点为B;直线l2:y2=kx+b经过点A和C(2,﹣1).
x+3经过点A(m,5),与y轴的交点为B;直线l2:y2=kx+b经过点A和C(2,﹣1).
(1)求直线l2的解析式,并直接写出不等式y1≥y2的解集;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点P到BE,BD,AC的距离恰好相等,则点P的位置:①在∠B的平分线上;②在∠DAC的平分线上;③在∠ECA的平分线上;④恰是∠B,∠DAC,∠ECA三条角平分线的交点,上述结论中,正确结论的个数有( )
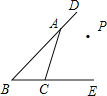
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
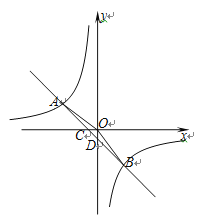
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于第二、四象限内的A,B两点,与x轴交于点C,与y轴交于点D,点B的坐标是(m,﹣4),连接AO,AO=5,sin∠AOC=
的图象交于第二、四象限内的A,B两点,与x轴交于点C,与y轴交于点D,点B的坐标是(m,﹣4),连接AO,AO=5,sin∠AOC=![]() .
.
(1)求反比例函数的解析式
(2)连接OB,求△AOB的面积
(3) 根据图象直接写出当![]() 时,x的取值范围.
时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图形的折叠即图形的翻折或者说是对称变换.这类问题与生活紧密联系,内容丰富,解法灵活,具有开放性,可以培养我们的动手能力,空间想象能力和几何变换的思想.在综合与实践课上,每个小组剪了一些如图1所示的直角三角形纸片(![]() ,
,![]() ,
,![]() ),并将
),并将![]() 纸片中的各内角进行折叠操作:
纸片中的各内角进行折叠操作:
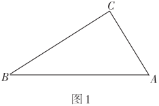
(1)如图2,“奋斗”小组将![]() 纸片中的
纸片中的![]() 进行折叠,使直角边
进行折叠,使直角边![]() 落在斜边
落在斜边![]() 上,点
上,点![]() 落在点
落在点![]() 位置,折痕为
位置,折痕为![]() ,则
,则![]() 的长为______
的长为______![]() .
.

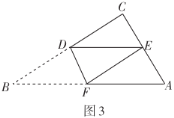
(2)如图3,“勤奋”小组将![]() 中的
中的![]() 进行折叠,使点
进行折叠,使点![]() 落在直角边
落在直角边![]() 中点
中点![]() 上,折痕为
上,折痕为![]() ,则
,则![]() 的长为______
的长为______![]() .
.
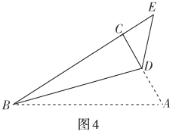
(3)如图4,“雄鹰”小组将![]() 纸片中的
纸片中的![]() 进行折叠,使点
进行折叠,使点![]() 落在直角边
落在直角边![]() 延长线上的点
延长线上的点![]() 处,折痕为
处,折痕为![]() ,求出
,求出![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是二次函数![]() 图象的一部分,图象过
图象的一部分,图象过![]() 点
点![]() ,二次函数图象对称轴为直线
,二次函数图象对称轴为直线![]() ,给出五个结论:①
,给出五个结论:①![]() ;②
;②![]() ;③
;③![]() ;④方程
;④方程![]() 的根为
的根为![]() ,
,![]() ;⑤当
;⑤当![]() 时,
时,![]() 随着
随着![]() 的增大而增大.其中正确结论是( )
的增大而增大.其中正确结论是( )

A. ①②③ B. ①③④ C. ②③④ D. ①④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从边长为a的大正方形纸板中挖去一个边长为b的小正方形后,将其裁成四个相同的等腰梯形(如图1),然后拼成一个平行四边形(如图2)。那么通过计算两个图形的阴影部分的面积,可以验证成立的公式是( )
A.a2-b2=(a-b)2 | B.(a+b)2="a+2ab+b" |
C.(a-b)2=a2-2ab+b2 | D.a2-b2=(a-b)(a+b) |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com