
【题目】如图所示是二次函数![]() 图象的一部分,图象过
图象的一部分,图象过![]() 点
点![]() ,二次函数图象对称轴为直线
,二次函数图象对称轴为直线![]() ,给出五个结论:①
,给出五个结论:①![]() ;②
;②![]() ;③
;③![]() ;④方程
;④方程![]() 的根为
的根为![]() ,
,![]() ;⑤当
;⑤当![]() 时,
时,![]() 随着
随着![]() 的增大而增大.其中正确结论是( )
的增大而增大.其中正确结论是( )

A. ①②③ B. ①③④ C. ②③④ D. ①④⑤
【答案】D
【解析】
根据抛物线的开口方向得a<0,对称轴在y轴右侧,得b>0,抛物线与y轴的正半轴相交,得c>0,故①正确;当x=1时,y=a+b+c>0,故②错误;当x=-2时,y=4a-2b+c<0,故③错误;根据对称轴为x=1,与x轴交于点(3,0)可得与x轴的另一个交点(-1,0),故④正确;由抛物线的对称性,得⑤正确.
∵抛物线的开口向下,
∴a<0,
∵对称轴x=1在y轴右侧,
∴b>0,
∵抛物线与y轴的正半轴相交,
∴c>0,故①正确;
当x=1时,y=a+b+c>0,故②错误;
当x=-2时,y=4a-2b+c<0,故③错误;
∵对称轴为x=1,与x轴交于点(3,0),
∴与x轴的另一个交点(-1,0),故④正确;
由图象得x<1时,y随着x的增大而增大,故⑤正确;
正确结论有①④⑤,
故选:D.


科目:初中数学 来源: 题型:
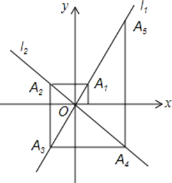
【题目】在平面角坐标系中,函数y=2x和y=-x的图像分别为直线l1、l2,过点(1,0)作x轴的垂线交l2于点A1,过点A1作y轴的垂线交l2于点A2,过点A2作x轴的垂线交l1于点A3,过点A3作y轴的垂线交l2于点A4,…,依次进行下去,则点A2020的坐标为_______________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在ABCD中,E是CD延长线上的一点,BE与AD交于点F,DE=![]() CD.
CD.
(1)求证:△ABF∽△CEB;
(2)若△DEF的面积为2,求ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列方程及其解的特征:
(1)![]() 的解为
的解为![]() ;
;
(2)![]() 的解为
的解为![]() ,
,![]() ;
;
(3)![]() 的解为
的解为![]() ,
,![]() ;
;
解答下列问题:
![]() 请猜想:方程
请猜想:方程![]() 的解为________;
的解为________;
![]() 请猜想:关于
请猜想:关于![]() 的方程
的方程![]() ________的解为
________的解为![]() ,
,![]() ;
;
![]() 下面以解方程
下面以解方程![]() 为例,验证
为例,验证![]() 中猜想结论的正确性.
中猜想结论的正确性.
解:原方程可化为![]() .
.
(下面请大家用配方法写出解此方程的详细过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与坐标轴分别交于点
与坐标轴分别交于点![]() 、
、![]() 和点
和点![]() ,动点
,动点![]() 从原点
从原点![]() 开始沿
开始沿![]() 方向以每秒
方向以每秒![]() 个单位长度移动,动点
个单位长度移动,动点![]() 从点
从点![]() 开始沿
开始沿![]() 方向以每秒
方向以每秒![]() 个单位长度移动,动点
个单位长度移动,动点![]() 、
、![]() 同时出发,当动点
同时出发,当动点![]() 到达原点
到达原点![]() 时,点
时,点![]() 、
、![]() 停止运动.
停止运动.

![]() 直接写出抛物线的解析式:________;
直接写出抛物线的解析式:________;
![]() 求
求![]() 的面积
的面积![]() 与
与![]() 点运动时间
点运动时间![]() 的函数解析式;当
的函数解析式;当![]() 为何值时,
为何值时,![]() 的面积最大?最大面积是多少?
的面积最大?最大面积是多少?
![]() 当
当![]() 的面积最大时,在抛物线上是否存在点
的面积最大时,在抛物线上是否存在点![]() (点
(点![]() 除外),使
除外),使![]() 的面积等于
的面积等于![]() 的最大面积?若存在,求出
的最大面积?若存在,求出![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王华、张伟两位同学分别将自己10次数学自我检测的成绩绘制成如下统计图:

(1)根据图中提供的数据列出如下统计表:
平均成绩(分) | 中位数(分) | 众数(分) | 方差(S2) | |
王华 | 80 | b | 80 | d |
张伟 | a | 85 | c | 260 |
则a= ,b= ,c= ,d= ,
(2)将90分以上(含90分)的成绩视为优秀,则优秀率高的是 .
(3)现在要从这两个同学选一位去参加数学竞赛,你可以根据以上的数据给老师哪些建议?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1).
(1)在图中作出![]() 关于
关于![]() 轴对称的
轴对称的![]() .
.
(2)写出点![]() 的坐标(直接写答案).
的坐标(直接写答案).
A1_____________,B1______________,C1______________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)方法感悟:如图①,在正方形ABCD中,点E、F分别为DC、BC边上的点,且满足∠EAF=45°,连接EF.将△ADE绕点A顺时针旋转90°得到△ABG,易证△GAF≌△EAF,从而得到结论:DE+BF=EF.根据这个结论,若CD=6,DE=2,求EF的长.

(2)方法迁移:如图②,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是BC、CD上的点,且∠EAF=![]() ∠BAD,试猜想DE,BF,EF之间有何数量关系,证明你的结论.
∠BAD,试猜想DE,BF,EF之间有何数量关系,证明你的结论.
(3)问题拓展:如图③,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,且∠EAF=![]() ∠BAD,试探究线段EF、BE、FD之间的数量关系,请直接写出你的猜想(不必说明理由).
∠BAD,试探究线段EF、BE、FD之间的数量关系,请直接写出你的猜想(不必说明理由).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com