
【题目】如图,在△![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上的点,
上的点,![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() ,垂足分别是
,垂足分别是![]() ,
,![]() ,若
,若![]() ,
,![]() ,那么下面四个结论:①
,那么下面四个结论:①![]() ;②
;②![]() //
//![]() ;③△
;③△![]() ≌△
≌△![]() ;④
;④![]() ,其中一定正确的是(填写编号)_____________.
,其中一定正确的是(填写编号)_____________.

【答案】①,②
【解析】
连接AP,根据角平分线性质即可推出①,根据勾股定理即可推出AR=AS,根据等腰三角形性质推出∠QAP=∠QPA,推出∠QPA=∠BAP,根据平行线判定推出QP∥AB即可;在Rt△BRP和Rt△QSP中,只有PR=PS.无法判断△BRP≌△QSP也无法证明![]() .
.
解:连接AP

①∵PR⊥AB,PS⊥AC,PR=PS,
∴点P在∠BAC的平分线上,∠ARP=∠ASP=90°,
∴∠SAP=∠RAP,
在Rt△ARP和Rt△ASP中,由勾股定理得:AR2=AP2-PR2,AS2=AP2-PS2,
∵AP=AP,PR=PS,
∴AR=AS,
∴①正确;
②∵AQ=QP,
∴∠QAP=∠QPA,
∵∠QAP=∠BAP,
∴∠QPA=∠BAP,
∴QP∥AR,
∴②正确;
③在Rt△BRP和Rt△QSP中,只有PR=PS,
不满足三角形全等的条件,故③④错误;
故答案为:①②.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.

(1)求证:△DEF是等腰三角形;
(2)当∠A=36°时,求∠DEF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
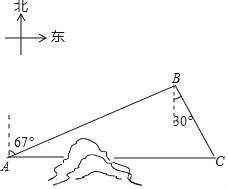
【题目】如图,C地在A地的正东方向,因有大山阻隔,由A地到C地需要绕行B地,已知B地位于A地北偏东67°方向,距离A地520km,C地位于B地南偏东30°方向,若打通穿山隧道,建成两地直达高铁,求A地到C地之间高铁线路的长(结果保留整数)
(参考数据:sin67°≈0.92;cos67°≈0.38;![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为平行四边形ABCD的边AD上的一点,E、F分别为PB、PC的中点,△PEF、△PDC、△PAB的面积分别为S、S1、S2.若S=3,则S1+S2的值为( )

A. 3 B. 6 C. 12 D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,某校数学兴趣小组为测得大厦AB的高度,在大厦前的平地上选择一点C,测得大厦顶端A的仰角为30°,再向大厦方向前进80米,到达点D处(C、D、B三点在同一直线上),又测得大厦顶端A的仰角为45°,请你计算该大厦的高度.(精确到0.1米,参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图与设计:
在图1和图2中,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.

(1)在图1中以格点为顶点画一个三角形,使三角形三边长分别为![]() ,
,![]() ,4;
,4;
(2)在图2中以格点为顶点画一个面积为10的正方形;
(3)在图3的正方形网格中建立平面直角坐标系,若![]() 各顶点的坐标分别为:
各顶点的坐标分别为:![]() ,
,![]() ,
,![]() ,请你作
,请你作![]() ,使
,使![]() 和
和![]() 关于
关于![]() 轴对称.
轴对称.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将每件进价为![]() 元的某种商品原来按每件
元的某种商品原来按每件![]() 元出售,一天可售出
元出售,一天可售出![]() 件.后来经过市场调查,发现这种商品单价每降低
件.后来经过市场调查,发现这种商品单价每降低![]() 元,其销量可增加
元,其销量可增加![]() 件.
件.
![]() 求商场经营该商品原来一天可获利润多少元?
求商场经营该商品原来一天可获利润多少元?
![]() 若商场经营该商品一天要获利润
若商场经营该商品一天要获利润![]() 元,并让顾客得到实惠,则每件商品应降价多少元?
元,并让顾客得到实惠,则每件商品应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,![]() ,AC=BC,D为BC的中点,过C作CE⊥AD于点E,延长CE交AB于点F,,连接FD;若AC=4,则CF+FD的值是( )
,AC=BC,D为BC的中点,过C作CE⊥AD于点E,延长CE交AB于点F,,连接FD;若AC=4,则CF+FD的值是( )

A.![]() B.5C.
B.5C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com