
【题目】如图,等边三角形![]() 的边长为4,
的边长为4,![]() 为边
为边![]() 上一点,过点
上一点,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,在
,在![]() 右侧作等边三角形
右侧作等边三角形![]() ,记
,记![]() 到
到![]() 的距离为
的距离为![]() ,
,![]() 到
到![]() 的距离为
的距离为![]() ,
,
(1)若![]() ,试求线段
,试求线段![]() 的长,并求m1、m2的值.
的长,并求m1、m2的值.
(2)若![]() ,用含
,用含![]() 的代数式表示
的代数式表示![]() ,
,![]() ,并求
,并求![]() 在∠C的平分线上时x的值.
在∠C的平分线上时x的值.

【答案】(1)DE=![]() ,m1=
,m1=![]() ,m2=0;(2)
,m2=0;(2)![]() ,
,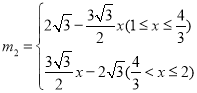 ,当
,当![]() 在
在![]() 的平分线上时x=1.
的平分线上时x=1.
【解析】
(1)过点![]() 作
作![]() ,则
,则![]() ,延长DP交AC于点G,由题意可得:△BED、△DFP、DGC、均为30°的直角三角形,由
,延长DP交AC于点G,由题意可得:△BED、△DFP、DGC、均为30°的直角三角形,由![]() 可得
可得![]() ,由等边三角形
,由等边三角形![]() 可得
可得![]() ,故
,故![]() 由于
由于![]() ,可得
,可得![]() 故
故![]() ;
;
(2)由(1)得当点P在三角形ABC内部时,![]() ;
;
①当![]() 时,点P在三角形ABC内部, 此时,同(1)中的思路;②当
时,点P在三角形ABC内部, 此时,同(1)中的思路;②当![]() 时,点P在三角形ABC一边上,同(1)可知
时,点P在三角形ABC一边上,同(1)可知![]() ,
,![]() ,
,
③当![]() 时,点P在三角形ABC外部时,过点
时,点P在三角形ABC外部时,过点![]() 做
做![]() ,则
,则![]() , DP与AC交于点G. 由题意可得:△BED、△DFP、DGC、均为30°的直角三角形可得
, DP与AC交于点G. 由题意可得:△BED、△DFP、DGC、均为30°的直角三角形可得![]() ,由等边三角形
,由等边三角形![]() 可得
可得![]() ,故
,故![]() ,
,
由DC=BC-BD=4-x可得![]() ,故
,故![]() ;当
;当![]() 在
在![]() 的平分线上时,此时
的平分线上时,此时![]() 在三角形内部
在三角形内部![]() ,有
,有![]() 列出方程
列出方程 ![]() 求解即可;
求解即可;
解:(1)如下图,过点![]() 作
作![]() ,则
,则![]() ,延长DP交AC于点G.
,延长DP交AC于点G.
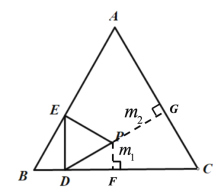
![]()
∵DE⊥BC,∠EDP=60°,
∴∠PDC=30°,
∵∠C=60°,
∴∠DGC=180°-∠PDC-∠C=90°,
∴![]() ,
,
∵![]() ,∠B=60°,∠BDE=90°,
,∠B=60°,∠BDE=90°,
∴![]() ,
,
∵![]() ,∠PDC=30°,PF⊥BC,
,∠PDC=30°,PF⊥BC,
∴![]() ,
,
∵![]() ,
,
且∠C=60°,PG⊥AC,
∴![]() ,
,
∴![]() ;
;
(2)由(1)得当点P在三角形ABC内部时,![]() ,
,
①当![]() 时,点P在三角形ABC内部,同(1)如下图,
时,点P在三角形ABC内部,同(1)如下图,

同(1)可证∠DGC=90°,
∴![]() ,
,
∵![]() ,∠B=60°,∠BDE=90°,
,∠B=60°,∠BDE=90°,
∴![]() ,
,
∵![]() ,∠PDC=30°,PF⊥BC,
,∠PDC=30°,PF⊥BC,
∴![]() ,
,
∵DC=BC-BD=4-x,
且∠C=60°,PG⊥AC,
∴![]() ,
,
∴![]() ,
,
②当![]() 时,点P在三角形ABC一边上,
时,点P在三角形ABC一边上,
同(1)可知![]() ,
,![]() ,
,
③当![]() 时,点P在三角形ABC外部,
时,点P在三角形ABC外部,
如下图,过点![]() 做
做![]() ,则
,则![]() , DP与AC交于点G.
, DP与AC交于点G.
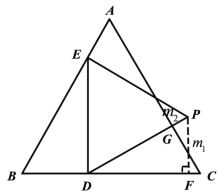
同(1)可证∠DGC=90°,
∴![]() ,
,
∵BD=x,∠B=60°,∠BDE=90°,
∴![]() ,
,
∵![]() ,∠PDC=30°,PF⊥BC,
,∠PDC=30°,PF⊥BC,
∴![]() ,
,
∵DC=BC-BD=4-x,
且∠C=60°,PG⊥AC,
∴![]() ,
,
∴![]() ,
,
综上所述, ,
,
当![]() 在
在![]() 的平分线上时,易知
的平分线上时,易知![]() 在三角形内部
在三角形内部![]() ,有
,有![]() ,
,
即 ![]() ,
,
解得 x=1;


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=60°,∠BAC的平分线AD与边BC的垂直平分线相交于点D,DE⊥AB交AB的延长线于点E,DF⊥AC于点F,现有下列结论:①DE=DF;②DE+DF=AD;③AM平分∠ADF;④AB+AC=2AE;其中正确的有( )

A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量河对岸l1上两棵古树A、B之间的距离,某数学兴趣小组在河这边沿着与AB平行的直线l2上取C、D两点,测得∠ACB=15°,∠ACD=45°,若l1、l2之间的距离为50m,则A、B之间的距离为( )
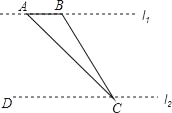
A. 50m B. 25m C. (50﹣![]() )m D. (50﹣25
)m D. (50﹣25![]() )m
)m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,CD=BE,DG⊥BC于点 G,EF⊥BC于点 F,且 DG=EF.

(1)求证:△DGC≌△EFB.
(2)连结 BD,CE. 求证:BD=CE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,线段AM为BC边上的高,D是AM上的点,以CD为一边,在CD的下方作等边△CDE,连结BE.
(1)填空:∠ACB=____;∠CAM=____;
(2)求证:△AOC≌△BEC;
(3)延长BE交射线AM于点F,请把图形补充完整,并求∠BFM的度数;
(4)当动点D在射线AM上,且在BC下方时,设直线BE与直线AM的交点为F.∠BFM的大小是否发生变化?若不变,请在备用图中面出图形,井直接写出∠BFM的度数;若变化,请写出变化规律.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(1,2)且与x轴交点的横坐标分别为x1,x2,其中﹣1<x1<0.1<x2<2.下列结论:4a+2b+c<0;2a+b<0;b2+8a>4ac;
a<﹣1;其中结论正确的有( )
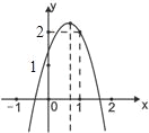
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.

(1)求证:△DEF是等腰三角形;
(2)当∠A=36°时,求∠DEF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图与设计:
在图1和图2中,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.

(1)在图1中以格点为顶点画一个三角形,使三角形三边长分别为![]() ,
,![]() ,4;
,4;
(2)在图2中以格点为顶点画一个面积为10的正方形;
(3)在图3的正方形网格中建立平面直角坐标系,若![]() 各顶点的坐标分别为:
各顶点的坐标分别为:![]() ,
,![]() ,
,![]() ,请你作
,请你作![]() ,使
,使![]() 和
和![]() 关于
关于![]() 轴对称.
轴对称.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com