
【题目】如图,点C是线段AB上一点,分别以AC和BC为边在线段AB的同侧作等边△ACD和△BCE,连结AE和BD,相交于点F.
(1)求证:AE=BD;
(2)如图2.固定△BCE不动,将等边△ACD绕点C旋转(△ACD和△BCE不重叠),试问∠AFB的大小是否变化?请说明理由;
(3)在△ACD旋转的过程中,以下结论:①CG=CH;② GF=HF; ③FC平分分∠GCH;④FC平分∠GFH;一定正确的有 (填写序号,不要求证明)


【答案】(1)见解析;(1)∠AFB的大小不变,理由见解析;(3)④
【解析】
(1)由∠ACD=∠BCE得到∠ACE=∠BCD,进而利用SAS得出△ACE≌△DCB进而得出答案;
(2)由△ACE≌△DCB得∠CBD=∠CEA,由三角形内角和定理得到结论∠AFB=180°-∠ACD=120°.
(3)根据等边三角形的性质,全等的判定与性质以及角平分线判定定理依次判断.
(1)证明:∵根据等边三角形的性质,可得∠ACD=∠BCE,
∴∠ACD+∠DCE=∠BCE+∠ECD,
即∠ACE=∠BCD.
在△ACE与△DCB中,

∴△ACE≌△DCB(SAS),
∴AE=BD;
(2)解:∠AFB的大小不变,理由如下:
∵△ACE≌△DCB,
∴∠CAE=∠CDB.
∵∠ADF=∠ADC+∠CDB,
∴∠ADF=∠ADC+∠CAE,
又∵∠AFB=∠FAD+∠ADF,
∴∠AFB=∠FAD+∠ADC+∠CAE,
∴∠AFB=∠DAC+∠ADC.
又∵∠DAC+∠ADC+∠ACD=180°,
∴∠DAC+∠ADC=180°-∠ACD,
∴∠AFB=180°-∠ACD,
∵∠ACD=60°,
∴∠AFB=120°.
所以∠AFB的大小不变.
(3)①②③在图1特殊情况下才成立,不一定正确;
④如图,过C作CM⊥AE于M,CN⊥BD于N,

∵△ACE≌△DCB,
∴BD=CE, S△ACE=S△DCB.
∴△BCD中BD边上的高与△ACE中AE边上的高对应相等,
即CM=CN,
∴点C在∠AFB的角平分线上,
即FC平分∠GFH,故④正确.


科目:初中数学 来源: 题型:
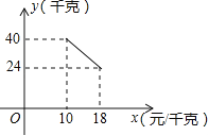
【题目】某经销商销售一种产品,这种产品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示:
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)该经销商想要每天获得150元的销售利润,销售价应定为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,CD=BE,DG⊥BC于点 G,EF⊥BC于点 F,且 DG=EF.

(1)求证:△DGC≌△EFB.
(2)连结 BD,CE. 求证:BD=CE
查看答案和解析>>
科目:初中数学 来源: 题型:
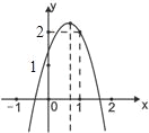
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(1,2)且与x轴交点的横坐标分别为x1,x2,其中﹣1<x1<0.1<x2<2.下列结论:4a+2b+c<0;2a+b<0;b2+8a>4ac;
a<﹣1;其中结论正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明周末要乘坐公交车到植物园游玩,从地图上查找路线发现,几条线路都需要换乘一次.在出发站点可选择空调车A、空调车B、普通车a,换乘站点可选择空调车C,普通车b、普通车c,且均在同一站点换乘.空调车投币2元,普通车投币1元.
(1)求小明在出发站点乘坐空调车的概率;
(2)求小明到达植物园恰好花费3元公交费的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.

(1)求证:△DEF是等腰三角形;
(2)当∠A=36°时,求∠DEF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是矩形ABCD的对角线AC的中点,E是AD的中点.若AB=6,AD=8,则四边形ABPE的周长为( )

A. 14 B. 16 C. 17 D. 18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为平行四边形ABCD的边AD上的一点,E、F分别为PB、PC的中点,△PEF、△PDC、△PAB的面积分别为S、S1、S2.若S=3,则S1+S2的值为( )

A. 3 B. 6 C. 12 D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)求证:AB=CD;
(2)若AB=CF,∠B=30°,求∠D的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com