
【题目】如图1,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于
轴交于![]() 、
、![]() 两点,
两点,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,点
,点![]() 为线段
为线段![]() 上一点,过点
上一点,过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,已知
,已知![]() ,
,![]() ,且
,且![]() 满足
满足![]() .
.
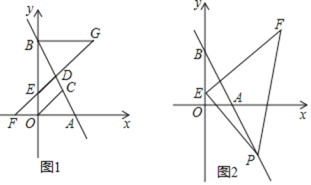
(1)求![]() 两点的坐标;
两点的坐标;
(2)若点![]() 为
为![]() 中点,延长
中点,延长![]() 交
交![]() 轴于点
轴于点![]() ,在
,在![]() 的延长线上取点
的延长线上取点![]() ,使
,使![]() ,连接
,连接![]() .
.
①![]() 与
与![]() 轴的位置关系怎样?说明理由;
轴的位置关系怎样?说明理由;
②求![]() 的长;
的长;
(3)如图2,若点![]() 的坐标为
的坐标为![]() ,
,![]() 是
是![]() 轴的正半轴上一动点,
轴的正半轴上一动点,![]() 是直线
是直线![]() 上一点,且
上一点,且![]() 的坐标为
的坐标为![]() ,是否存在点
,是否存在点![]() 使
使![]() 为等腰直角三角形?若存在,求出点
为等腰直角三角形?若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
【答案】(1)点A的坐标为(3,0),点B的坐标为(0,6);(2)①BG⊥y轴,理由见解析;②![]() ;(3)存在,点E的坐标为(0,4)
;(3)存在,点E的坐标为(0,4)
【解析】
(1)根据平方和绝对值的非负性即可求出m和n的值,从而求出点A、B的坐标;
(2)①利用SAS即可证出△BDG≌△ADF,从而得出∠G=∠AFD,根据平行线的判定可得BG∥AF,从而得出∠GBO=90°,即可得出结论;
②过点D作DM⊥x轴于M,根据平面直角坐标系中线段的中点公式即可求出点D的坐标,从而求出OM=![]() ,DM=3,根据角平分线的定义可得∠COA=45°,再根据平行线的性质和等腰三角形的判定可得△FMD为等腰三角形,FM=DM=3,从而求出点F的坐标;
,DM=3,根据角平分线的定义可得∠COA=45°,再根据平行线的性质和等腰三角形的判定可得△FMD为等腰三角形,FM=DM=3,从而求出点F的坐标;
(3)过点F作FG⊥y轴于G,过点P作PH⊥y轴于H,利用AAS证出△GFE≌△HEP,从而得出FG=EH,GE=PH,然后根据点F和点P的坐标即可求出OE的长,从而求出点E的坐标.
解:(1)∵![]() ,
,![]()
∴![]()
解得:![]()
∴AO=3,BO=6
∴点A的坐标为(3,0),点B的坐标为(0,6);
(2)①BG⊥y轴,理由如下
∵点![]() 为
为![]() 中点
中点
∴BD=AD
在△BDG和△ADF中
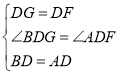
∴△BDG≌△ADF
∴∠G=∠AFD
∴BG∥AF
∴∠GBO=180°-∠AOB=90°
∴BG⊥y轴;
②过点D作DM⊥x轴于M
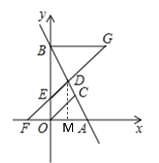
∵点![]() 为
为![]() 中点
中点
∴点D的坐标为(![]() )=(
)=(![]() )
)
∴OM=![]() ,DM=3
,DM=3
∵![]() 平分
平分![]()
∴∠COA=![]()
∵![]()
∴∠MFD=∠COA=45°
∴△FMD为等腰三角形,FM=DM=3
∴OF=FM-OM=![]() ;
;
(3)存在,
过点F作FG⊥y轴于G,过点P作PH⊥y轴于H
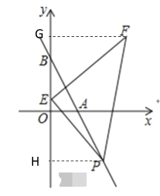
若![]() 为等腰直角三角形,必有EF=PE,∠FEP=90°
为等腰直角三角形,必有EF=PE,∠FEP=90°
∴∠GFE+∠GEF=90°,∠HEP+∠GEF=90°
∴∠GFE=∠HEP
在△GFE和△HEP中
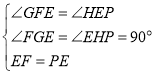
∴△GFE≌△HEP
∴FG=EH,GE=PH
∵点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]()
∴OG=10,PH=6
∴GE=6
∴OE=OG-GE=4
∴点E的坐标为(0,4).


科目:初中数学 来源: 题型:
【题目】《九章算术》是中国古代数学的重要著作,方程术是它的最高成就,其中记载:今有牛五、羊二,直金十两;牛二、羊五,直金八两.问:牛、羊各直金几何?”译文:“假设有5头牛、2只羊,值金10两;2头牛、5只羊,值金8两.问:每头牛、每只羊各值金多少两?”设每头牛值金x两,每只羊值金y两,则列方程组错误的是( )

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
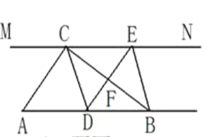
【题目】如图,在Rt△ABC中,∠ACB=90,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE
(1)求证:CE=AD
(2)当点D在AB中点时,四边形BECD是什么特殊四边形?说明理由
(3)若D为AB的中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,点
,点![]() 将线段
将线段![]() 分成两部分,如果
分成两部分,如果![]() ,那么称点
,那么称点![]() 为线段
为线段![]() 的黄金分割点,某教学兴趣小组在进行研究时,由“黄金分割点”联想到“黄金分割线”,类似的给出“黄金分割线”的定义:“一直线将一个面积为
的黄金分割点,某教学兴趣小组在进行研究时,由“黄金分割点”联想到“黄金分割线”,类似的给出“黄金分割线”的定义:“一直线将一个面积为![]() 的图形分成两部分,这两部分的面积分别为
的图形分成两部分,这两部分的面积分别为![]() ,
,![]() ,如果
,如果![]() ,那么称这条直线为该图形的黄金分割线.
,那么称这条直线为该图形的黄金分割线.
![]() 如图
如图![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,
,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,请问直线
,请问直线![]() 是不是
是不是![]() 的黄金分割线,并证明你的结论;
的黄金分割线,并证明你的结论;
![]() 如图
如图![]() ,在边长为
,在边长为![]() 的正方形
的正方形![]() 中,点
中,点![]() 是边
是边![]() 上一点,若直线
上一点,若直线![]() 是正方形
是正方形![]() 的黄金分割线,求
的黄金分割线,求![]() 的长.
的长.
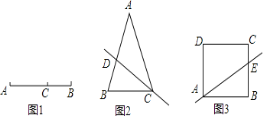
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某品牌计算机春节期间搞活动,规定每台计算机售价 0.7 万元,首次付款后每个月应还的钱数 y (元)与还钱月数 t 的关系如图所示.
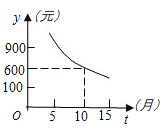
(1)根据图像写出 y 与 t 的函数关系式;
(2)求出首次付款的钱数;
(3)如果要求每月支付的钱数不多于 400 元,那么首付后还至少需几个月才能将所有的钱全部还清?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三位运动员在相同条件下各射靶10次,每次射靶的成绩如下:
甲:9,10,8,5,7,8,10,8,8,7
乙:5,7,8,7,8,9,7,9,10,10
丙:7,6,8,5,4,7,6,3,9,5
(1)根据以上数据完成下表:
平均数 | 中位数 | 方差 | |
甲 | 8 | 8 | ________ |
乙 | ________ | 8 | 2.2 |
丙 | 6 | ________ | 3 |
(2)根据表中数据分析,哪位运动员的成绩最稳定,并简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 在平面直角坐标系中的位置如图所示.
在平面直角坐标系中的位置如图所示.

(1)作出![]() 关于
关于![]() 轴对称的
轴对称的![]() ,并写出
,并写出![]() 各顶点的坐标;
各顶点的坐标;
(2)将![]() 向右平移6个单位,作出平移后的
向右平移6个单位,作出平移后的![]() 并写出
并写出![]() 各顶点的坐标;
各顶点的坐标;
(3)观察![]() 和
和![]() ,它们是否关于某直线对称?若是,请用粗线条画出对称轴.
,它们是否关于某直线对称?若是,请用粗线条画出对称轴.
查看答案和解析>>
科目:初中数学 来源: 题型:
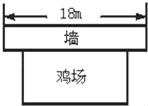
【题目】如图某农场要建一个长方形的养鸡场,鸡场的一边靠墙(墙长18m),另三边用木栏围成,木栏长35m.鸡场的面积能达到150m2吗?如果能,请你给出设计方案;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
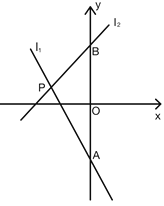
【题目】如图,已知直线![]() ,直线
,直线![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() 分别与
分别与![]() 轴相交于点
轴相交于点![]() .
.
(1)求点P的坐标.
(2)若![]() ,求x的取值范围.
,求x的取值范围.
(3)点![]() 为x轴上的一个动点,过
为x轴上的一个动点,过![]() 作x轴的垂线分别交
作x轴的垂线分别交![]() 和
和![]() 于点
于点![]() ,当EF=3时,求m的值.
,当EF=3时,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com