
【题目】如图![]() ,点
,点![]() 将线段
将线段![]() 分成两部分,如果
分成两部分,如果![]() ,那么称点
,那么称点![]() 为线段
为线段![]() 的黄金分割点,某教学兴趣小组在进行研究时,由“黄金分割点”联想到“黄金分割线”,类似的给出“黄金分割线”的定义:“一直线将一个面积为
的黄金分割点,某教学兴趣小组在进行研究时,由“黄金分割点”联想到“黄金分割线”,类似的给出“黄金分割线”的定义:“一直线将一个面积为![]() 的图形分成两部分,这两部分的面积分别为
的图形分成两部分,这两部分的面积分别为![]() ,
,![]() ,如果
,如果![]() ,那么称这条直线为该图形的黄金分割线.
,那么称这条直线为该图形的黄金分割线.
![]() 如图
如图![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,
,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,请问直线
,请问直线![]() 是不是
是不是![]() 的黄金分割线,并证明你的结论;
的黄金分割线,并证明你的结论;
![]() 如图
如图![]() ,在边长为
,在边长为![]() 的正方形
的正方形![]() 中,点
中,点![]() 是边
是边![]() 上一点,若直线
上一点,若直线![]() 是正方形
是正方形![]() 的黄金分割线,求
的黄金分割线,求![]() 的长.
的长.
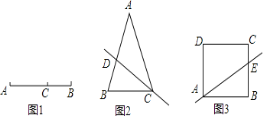
【答案】![]() 直线
直线![]() 是
是![]() 的黄金分割线,理由见解析;(2)
的黄金分割线,理由见解析;(2)![]() 长为
长为![]() .
.
【解析】
(1)如图2,根据等高三角形的面积比等于底的比可得![]() ,
,![]() ,
,
要证直线CD是△ABC的黄金分割线,只需证![]() ,只需证
,只需证![]() ,易证BC=AD,只需证
,易证BC=AD,只需证![]() ,只需证△BCD∽△BAC即可;
,只需证△BCD∽△BAC即可;
(2)设BE=x,如图3,易得![]() ,
,![]() ,
,![]() .由直线AE是正方形ABCD的黄金分割线可得
.由直线AE是正方形ABCD的黄金分割线可得![]() ,由此得到关于x的方程,解这个方程就可解决问题.
,由此得到关于x的方程,解这个方程就可解决问题.
解:![]() 直线
直线![]() 是
是![]() 的黄金分割线.
的黄金分割线.
理由:如图![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() .
.
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,

∴![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴直线![]() 是
是![]() 的黄金分割线;
的黄金分割线;
![]() 设
设![]() ,如图
,如图![]() ,
,
∵正方形![]() 的边长为
的边长为![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() .
.
∵直线![]() 是正方形
是正方形![]() 的黄金分割线,
的黄金分割线,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
整理得:![]() ,
,
解得:![]() ,
,![]() .
.
∵点![]() 是边
是边![]() 上一点,
上一点,
∴![]() ,
,
∴![]() ,
,
∴![]() 长为
长为![]() .
.


科目:初中数学 来源: 题型:
【题目】我国的农作物主要以水稻、玉米和小麦为主,种植太单调不利于土壤环境的维护,而且对农业的发展也没有促进作用,为了鼓励大豆的种植,国家对种植大豆的农民给予补贴,调动农民种植大豆的积极性.我市乃大豆之乡,今年很多合作社调整种植结构,把种植玉米改成种植大豆,今年我市某合作社共收获大豆200吨,计划采用批发和零售两种方式销售.经市场调查,批发平均每天售出14吨,由于今年我市小型大豆深加工企业的增多,预计能提前完成销售任务,在平均每天批发量不变的情况下,实际平均每天的零售量比原计划的2倍还多14吨,结果提前5天完成销售任务。那么原计划零售平均每天售出多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边三角形ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ.
(1)求证:△ABP≌△ACQ;
(2)请判断△APQ是什么三角形,试说明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数![]() (x>0)的图象交于A(2,﹣1),B(
(x>0)的图象交于A(2,﹣1),B(![]() ,n)两点,直线y=2与y轴交于点C.
,n)两点,直线y=2与y轴交于点C.

(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点![]() 和点
和点![]() ,点
,点![]() 和点
和点![]() 是
是![]() 轴上的两个定点.
轴上的两个定点.
(1)当线段![]() 向左平移到某个位置时,若
向左平移到某个位置时,若![]() 的值最小,求平移的距离.
的值最小,求平移的距离.
(2)当线段![]() 向左或向右平移时,是否存在某个位置,使四边形
向左或向右平移时,是否存在某个位置,使四边形![]() 的周长最小?请说明如何平移?若不存在,请说明理由.
的周长最小?请说明如何平移?若不存在,请说明理由.
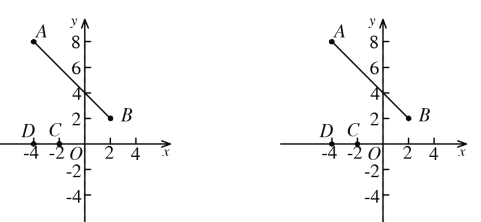
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:对于一些次数较高或者是比较复杂的式子进行因式分解时,换元法是一种常用的方法,下面是某同学用换元法对多项式![]() 进行因式分解的过程.
进行因式分解的过程.
解:设![]()
原式![]() (第一步)
(第一步)
![]() (第二步)
(第二步)
![]() (第三步)
(第三步)
![]() (第四步)
(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的__________(填代号).
A.提取公因式 B.平方差公式
C.两数和的完全平方公式 D.两数差的完全平方公式
(2)按照“因式分解,必须进行到每一个多项式因式都不能再分解为止”的要求,该多项式分解因式的最后结果为______________.
(3)请你模仿以上方法对多项式![]() 进行因式分解.
进行因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于
轴交于![]() 、
、![]() 两点,
两点,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,点
,点![]() 为线段
为线段![]() 上一点,过点
上一点,过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,已知
,已知![]() ,
,![]() ,且
,且![]() 满足
满足![]() .
.
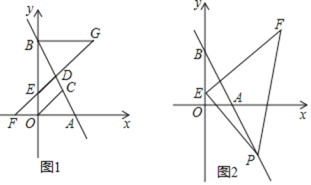
(1)求![]() 两点的坐标;
两点的坐标;
(2)若点![]() 为
为![]() 中点,延长
中点,延长![]() 交
交![]() 轴于点
轴于点![]() ,在
,在![]() 的延长线上取点
的延长线上取点![]() ,使
,使![]() ,连接
,连接![]() .
.
①![]() 与
与![]() 轴的位置关系怎样?说明理由;
轴的位置关系怎样?说明理由;
②求![]() 的长;
的长;
(3)如图2,若点![]() 的坐标为
的坐标为![]() ,
,![]() 是
是![]() 轴的正半轴上一动点,
轴的正半轴上一动点,![]() 是直线
是直线![]() 上一点,且
上一点,且![]() 的坐标为
的坐标为![]() ,是否存在点
,是否存在点![]() 使
使![]() 为等腰直角三角形?若存在,求出点
为等腰直角三角形?若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
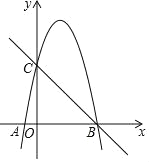
【题目】如图,抛物线y=﹣x2+4x+5与x轴,y轴分别交于A,B,C三点.
(1)请直接写出A,B,C三点坐标:A(_____,_____)、B(_____,______)、C(______,______)
(2)若⊙M过A、B、C三点,求圆心M的坐标,并求⊙M的面积;
(3)在(2)的条件下,在抛物线上是否存在点N,使得由A,C,M,N四点构成的四边形为平行四边形?若存在,请求出点N的坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com