练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

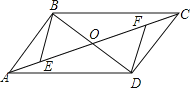
    【题目】如图，ABCD的对角线AC、BD相交于点O，OE＝OF．

    （1）求证：△BOE≌△DOF；

    （2）若BD＝EF，连接DE、BF，判断四边形EBFD的形状，并说明理由．

    【答案】（1）见解析；（2）四边形EBFD是矩形；理由见解析

    【解析】

    （1）由平行四边形的性质得出OB＝OD，由SAS证明△BOE≌△DOF即可；

    （2）先证明四边形EBFD是平行四边形，再由对角线相等即可得出四边形EBFD是矩形．

    （1）证明：∵四边形ABCD是平行四边形，

    ∴OB＝OD，

    在△BOE和△DOF中，，

    ∴△BOE≌△DOF（SAS）；

    （2）解：四边形EBFD是矩形；理由如下：如图所示：

    ∵OB＝OD，OE＝OF，

    ∴四边形EBFD是平行四边形，

    又∵BD＝EF，

    ∴四边形EBFD是矩形．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某校开展“我最喜爱的一项体育活动”调查，要求每名学生必选且只能选一项，现随机抽查了m名学生，并将其结果绘制成如下不完整的条形图和扇形图，请结合以上信息解答下列问题：

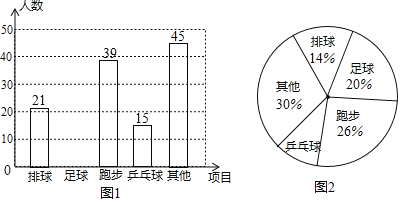
    （1）求m的值；

    （2）请补全上面的条形统计图；

    （3）在图2中，“乒乓球”所对应扇形的圆心角的度数为多少度？

    （4）已知该校共有1200名学生，请你估计该校约有多少名学生最喜爱足球活动？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

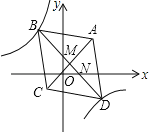
    【题目】如图，在平面直角坐标系xOy中，菱形ABCD的顶点A（4，4），C（﹣2，﹣2），点B，D在反比例函数的图象上，对角线BD交AC于点M，交x轴于点N，若，则k的值是_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为拓宽学生视野，我市某中学决定组织部分师生去庐山西海开展研学旅行活动，在参加此次活动的师生中，若每位老师带17个学生，还剩12个学生没人带；若每位老师带18个学生，就有一位老师少带4个学生．为了安全，既要保证所有师生都有车坐，又要保证每辆客车上至少要有2名老师．现有甲、乙两种大客车，它们的载客量和租金如表所示．

    甲种客车

    乙种客车

    载客量/（人/辆）

    30

    42

    租金/（元/辆）

    300

    400

    （1）参加此次研学旅行活动的老师和学生各有多少人？租用客车总数为多少辆？

    （2）设租用x辆乙种客车，租车总费用为w元，请写出w与x之间的函数关系式；

    （3）在（2）的条件下，学校计划此次研学旅行活动的租车总费用不超过3100元，租用乙种客车不少5辆，你能得出哪几种不同的租车方案？其中哪种租车方案最省钱？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

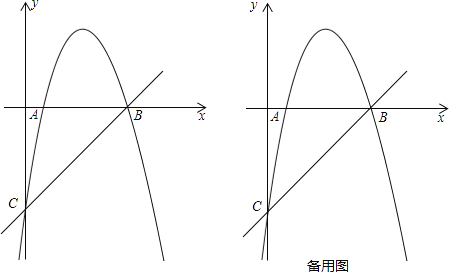
    【题目】如图，抛物线y=ax2+6x+c交x轴于A，B两点，交y轴于点C．直线y=x﹣5经过点B，C．

    （1）求抛物线的解析式；

    （2）过点A的直线交直线BC于点M．

    ①当AM⊥BC时，过抛物线上一动点P（不与点B，C重合），作直线AM的平行线交直线BC于点Q，若以点A，M，P，Q为顶点的四边形是平行四边形，求点P的横坐标；

    ②连接AC，当直线AM与直线BC的夹角等于∠ACB的2倍时，请直接写出点M的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一辆汽车在某次行驶过程中，油箱中的剩余油量y（升）与行驶路程x（千米）之间是一次函数关系，其部分图象如图所示．

    （1）求y关于x的函数关系式；（不需要写定义域）

    （2）已知当油箱中的剩余油量为8升时，该汽车会开始提示加油，在此次行驶过程中，行驶了500千米时，司机发现离前方最近的加油站有30千米的路程，在开往该加油站的途中，汽车开始提示加油，这时离加油站的路程是多少千米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

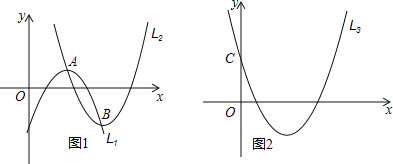
    【题目】如图1，若抛物线L1的顶点A在抛物线L2上，抛物线L2的顶点B也在抛物线L1上（点A与点B不重合）我们把这样的两抛物线L1、L2互称为“友好”抛物线，可见一条抛物线的“友好”抛物线可以有很多条．

    （1）如图2，已知抛物线L3：y=2x2-8x+4与y轴交于点C，试求出点C关于该抛物线对称轴对称的对称点D的坐标；

    （2）请求出以点D为顶点的L3的“友好”抛物线L4的解析式，并指出L3与L4中y同时随x增大而增大的自变量的取值范围；

    （3）若抛物y=a1（x-m）2+n的任意一条“友好”抛物线的解析式为y=a2（x-h）2+k，请写出a1与a2的关系式，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

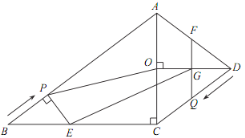
    【题目】已知：如图，在四边形 ABCD 中， AB∥CD， ACB =90°， AB=10cm， BC=8cm， OD 垂直平分 A C．点 P 从点 B 出发，沿 BA 方向匀速运动，速度为 1cm/s；同时，点 Q 从点 D 出发，沿 DC 方向匀速运动，速度为 1cm/s；当一个点停止运动，另一个点也停止运动．过点 P作 PE⊥AB，交 BC 于点 E，过点 Q 作 QF∥AC，分别交 AD， OD 于点 F， G．连接 OP，EG．设运动时间为 t ( s )（0＜t＜5） ，解答下列问题：

    （1）当 t 为何值时，点 E 在 BAC 的平分线上？

    （2）设四边形 PEGO 的面积为 S(cm2) ，求 S 与 t 的函数关系式；

    （3）在运动过程中，是否存在某一时刻 t ，使四边形 PEGO 的面积最大？若存在，求出t 的值；若不存在，请说明理由；

    （4）连接 OE， OQ，在运动过程中，是否存在某一时刻 t ，使 OE⊥OQ？若存在，求出t 的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】现有一组数据：165、160、166、170、164、165，若去掉最后一个数165，下列说法正确的是（　　）

    A. 平均数不变，方差变大B. 平均数不变，方差不变

    C. 平均数不变，方差变小D. 平均数变小，方差不变

    查看答案和解析>>

    同步练习册答案