
【题目】如图,抛物线y=ax2+6x+c交x轴于A,B两点,交y轴于点C.直线y=x﹣5经过点B,C.
(1)求抛物线的解析式;
(2)过点A的直线交直线BC于点M.
①当AM⊥BC时,过抛物线上一动点P(不与点B,C重合),作直线AM的平行线交直线BC于点Q,若以点A,M,P,Q为顶点的四边形是平行四边形,求点P的横坐标;
②连接AC,当直线AM与直线BC的夹角等于∠ACB的2倍时,请直接写出点M的坐标.
【答案】(1)抛物线解析式为y=﹣x2+6x﹣5;(2)①P点的横坐标为4或![]() 或
或![]() ;②点M的坐标为(
;②点M的坐标为(![]() ,﹣
,﹣![]() )或(
)或(![]() ,﹣
,﹣![]() ).
).
【解析】(1)利用一次函数解析式确定C(0,-5),B(5,0),然后利用待定系数法求抛物线解析式;
(2)①先解方程-x2+6x-5=0得A(1,0),再判断△OCB为等腰直角三角形得到∠OBC=∠OCB=45°,则△AMB为等腰直角三角形,所以AM=2![]() ,接着根据平行四边形的性质得到PQ=AM=2
,接着根据平行四边形的性质得到PQ=AM=2![]() ,PQ⊥BC,作PD⊥x轴交直线BC于D,如图1,利用∠PDQ=45°得到PD=
,PQ⊥BC,作PD⊥x轴交直线BC于D,如图1,利用∠PDQ=45°得到PD=![]() PQ=4,设P(m,-m2+6m-5),则D(m,m-5),讨论:当P点在直线BC上方时,PD=-m2+6m-5-(m-5)=4;当P点在直线BC下方时,PD=m-5-(-m2+6m-5),然后分别解方程即可得到P点的横坐标;
PQ=4,设P(m,-m2+6m-5),则D(m,m-5),讨论:当P点在直线BC上方时,PD=-m2+6m-5-(m-5)=4;当P点在直线BC下方时,PD=m-5-(-m2+6m-5),然后分别解方程即可得到P点的横坐标;
②作AN⊥BC于N,NH⊥x轴于H,作AC的垂直平分线交BC于M1,交AC于E,如图2,利用等腰三角形的性质和三角形外角性质得到∠AM1B=2∠ACB,再确定N(3,-2),
AC的解析式为y=5x-5,E点坐标为(![]() ,-
,-![]() ),利用两直线垂直的问题可设直线EM1的解析式为y=-
),利用两直线垂直的问题可设直线EM1的解析式为y=-![]() x+b,把E(
x+b,把E(![]() ,-
,-![]() )代入求出b得到直线EM1的解析式为y=-
)代入求出b得到直线EM1的解析式为y=-![]() x-
x-![]() ,则解方程组
,则解方程组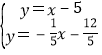 得M1点的坐标;作直线BC上作点M1关于N点的对称点M2,如图2,利用对称性得到∠AM2C=∠AM1B=2∠ACB,设M2(x,x-5),根据中点坐标公式得到3=
得M1点的坐标;作直线BC上作点M1关于N点的对称点M2,如图2,利用对称性得到∠AM2C=∠AM1B=2∠ACB,设M2(x,x-5),根据中点坐标公式得到3=![]() ,然后求出x即可得到M2的坐标,从而得到满足条件的点M的坐标.
,然后求出x即可得到M2的坐标,从而得到满足条件的点M的坐标.
(1)当x=0时,y=x﹣5=﹣5,则C(0,﹣5),
当y=0时,x﹣5=0,解得x=5,则B(5,0),
把B(5,0),C(0,﹣5)代入y=ax2+6x+c得
![]() ,解得
,解得![]() ,
,
∴抛物线解析式为y=﹣x2+6x﹣5;
(2)①解方程﹣x2+6x﹣5=0得x1=1,x2=5,则A(1,0),
∵B(5,0),C(0,﹣5),
∴△OCB为等腰直角三角形,
∴∠OBC=∠OCB=45°,
∵AM⊥BC,
∴△AMB为等腰直角三角形,
∴AM=![]() AB=
AB=![]() ×4=2
×4=2![]() ,
,
∵以点A,M,P,Q为顶点的四边形是平行四边形,AM∥PQ,
∴PQ=AM=2![]() ,PQ⊥BC,
,PQ⊥BC,
作PD⊥x轴交直线BC于D,如图1,则∠PDQ=45°,
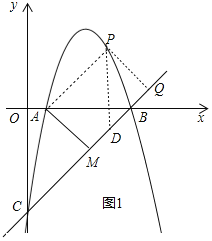
∴PD=![]() PQ=
PQ=![]() ×2
×2![]() =4,
=4,
设P(m,﹣m2+6m﹣5),则D(m,m﹣5),
当P点在直线BC上方时,
PD=﹣m2+6m﹣5﹣(m﹣5)=﹣m2+5m=4,解得m1=1,m2=4,
当P点在直线BC下方时,
PD=m﹣5﹣(﹣m2+6m﹣5)=m2﹣5m=4,解得m1=![]() ,m2=
,m2=![]() ,
,
综上所述,P点的横坐标为4或![]() 或
或![]() ;
;
②作AN⊥BC于N,NH⊥x轴于H,作AC的垂直平分线交BC于M1,交AC于E,如图2,
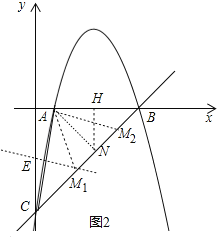
∵M1A=M1C,
∴∠ACM1=∠CAM1,
∴∠AM1B=2∠ACB,
∵△ANB为等腰直角三角形,
∴AH=BH=NH=2,
∴N(3,﹣2),
易得AC的解析式为y=5x﹣5,E点坐标为(![]() ,﹣
,﹣![]() ,
,
设直线EM1的解析式为y=﹣![]() x+b,
x+b,
把E(![]() ,﹣
,﹣![]() )代入得﹣
)代入得﹣![]() +b=﹣
+b=﹣![]() ,解得b=﹣
,解得b=﹣![]() ,
,
∴直线EM1的解析式为y=﹣![]() x﹣
x﹣![]()
解方程组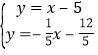 得
得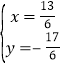 ,则M1(
,则M1(![]() ,﹣
,﹣![]() );
);
作直线BC上作点M1关于N点的对称点M2,如图2,则∠AM2C=∠AM1B=2∠ACB,
设M2(x,x﹣5),
∵3=![]()
∴x=![]() ,
,
∴M2(![]() ,﹣
,﹣![]() ).
).
综上所述,点M的坐标为(![]() ,﹣
,﹣![]() )或(
)或(![]() ,﹣
,﹣![]() ).
).


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+2x+3与x轴交于点A,C(点A在点C的右侧),与y轴交于点B
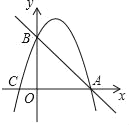
(1)求点A,B的坐标及直线AB的函数表达式;
(2)若直线l⊥x轴,且直线l在第一象限内与抛物线交于点M,与直线AB交于点N,求点M与点N之间的距离的最大值,并求出此时点M,N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某品牌手机去年每台的售价y(元)与月份x之间满足函数关系:y=﹣50x+2600,去年的月销量p(万台)与月份x之间成一次函数关系,其中1﹣6月份的销售情况如下表:
月份(x) | 1月 | 2月 | 3月 | 4月 | 5月 | 6月 |
销售量(p) | 3.9万台 | 4.0万台 | 4.1万台 | 4.2万台 | 4.3万台 | 4.4万台 |
(1)求p关于x的函数关系式;
(2)求该品牌手机在去年哪个月的销售金额最大?最大是多少万元?
(3)今年1月份该品牌手机的售价比去年12月份下降了m%,而销售量也比去年12月份下降了1.5m%.今年2月份,经销商决定对该手机以1月份价格的“八折”销售,这样2月份的销售量比今年1月份增加了1.5万台.若今年2月份这种品牌手机的销售额为6400万元,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
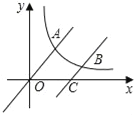
【题目】如图,直线y=![]() x与双曲线y=
x与双曲线y=![]() (x>0)交于点A,将直线y=
(x>0)交于点A,将直线y=![]() x向下平移个6单位后,与双曲线y=
x向下平移个6单位后,与双曲线y=![]() (x>0)交于点B,与x轴交于点C,则C点的坐标为_____;若
(x>0)交于点B,与x轴交于点C,则C点的坐标为_____;若![]() =2,则k=_____.
=2,则k=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上),已知AB=80 m,DE=10 m,求障碍物B,C两点间的距离.(结果精确到0.1 m)(参考数据: ![]() ≈1.414,、
≈1.414,、![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某数学兴趣小组在活动课上测量学校旗杆的高度.已知小亮站着测量,眼睛与地面的距离(AB)是1.7米,看旗杆顶部E的仰角为30°;小敏蹲着测量,眼睛与地面的距离(CD)是0.7米,看旗杆顶部E的仰角为45°.两人相距5米且位于旗杆同侧(点B、D、F在同一直线上).
(1)求小敏到旗杆的距离DF.(结果保留根号)
(2)求旗杆EF的高度.(结果保留整数,参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7)
≈1.7)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:![]() ,则大楼AB的高度约为( )(精确到0.1米,参考数据:
,则大楼AB的高度约为( )(精确到0.1米,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.45)
≈2.45)

A. 30.6 B. 32.1 C. 37.9 D. 39.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
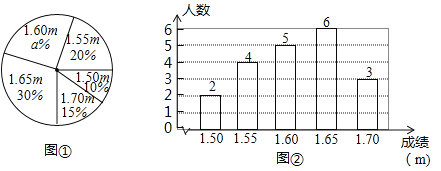
(Ⅰ)图①中![]() 的值为__________;
的值为__________;
(Ⅱ)求统计的这组初赛成绩数据的平均数、众数和中位数;
(Ⅲ)根据这组初赛成绩,由高到低确定10人能进入复赛,请直接写出初赛成绩为![]() 的运动员能否进入复赛.
的运动员能否进入复赛.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com