
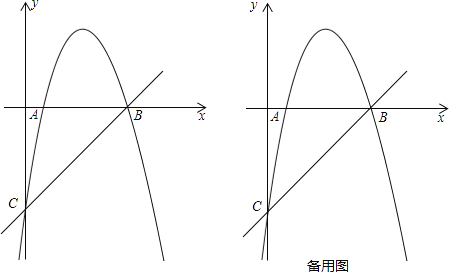
【题目】如图,抛物线y=﹣x2+2x+3与x轴交于点A,C(点A在点C的右侧),与y轴交于点B
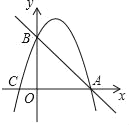
(1)求点A,B的坐标及直线AB的函数表达式;
(2)若直线l⊥x轴,且直线l在第一象限内与抛物线交于点M,与直线AB交于点N,求点M与点N之间的距离的最大值,并求出此时点M,N的坐标.
【答案】(1)A(3,0),B(0,3),y=﹣x+3;(2)MN有最大值![]() ,M
,M![]() ,N
,N![]() .
.
【解析】
(1)求出B(0,3),A(3,0),C(﹣1,0),待定系数法求解析式;
(2)M(a,﹣a2+2a+3),N(a,﹣a+3),M在点N的上方,MN=﹣a2+2a+3﹣(﹣a+3)=﹣(a﹣![]() )2+
)2+![]() ,由0<a<3,即可求MN的最大值;
,由0<a<3,即可求MN的最大值;
(1)由y=﹣x2+2x+3可得:
B(0,3),A(3,0),C(﹣1,0),
设直线AB的解析式y=kx+b,
∴![]() ,
,
∴![]() ,
,
∴y=﹣x+3;
(2)设直线l的解析式为x=a,
∴0<a<3,
∴M(a,﹣a2+2a+3),N(a,﹣a+3),
∵MN在第一象限,
∴点M在点N的上方,
∴MN=﹣a2+2a+3﹣(﹣a+3)=﹣(a﹣![]() )2+
)2+![]() ,
,
∴当a=![]() 时,MN有最大值
时,MN有最大值![]() ,
,
∴N(![]() ,
,![]() ),M(
),M(![]() ,
,![]() );
);


科目:初中数学 来源: 题型:
【题目】受地震的影响,某超市鸡蛋供应紧张,需每天从外地调运鸡蛋1200斤.超市决定从甲、乙两大型养殖场调运鸡蛋,已知甲养殖场每天最多可调出800斤,乙养殖场每天最多可调出900斤,从两养殖场调运鸡蛋到超市的路程和运费如表:
到超市的路程(千米) | 运费(元/斤千米) | |
甲养殖场 | 200 | 0.012 |
乙养殖场 | 140 | 0.015 |
(1)若某天调运鸡蛋的总运费为2670元,则从甲、乙两养殖场各调运了多少斤鸡蛋?
(2)设从甲养殖场调运鸡蛋x斤,总运费为W元,试写出W与x的函数关系式,怎样安排调运方案才能使每天的总运费最省?
查看答案和解析>>
科目:初中数学 来源: 题型:
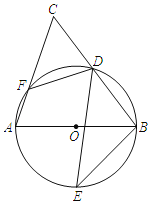
【题目】如图,AB是⊙O的直径,D,E为⊙O上位于AB异侧的两点,连结BD并延长至点C,使得CD=BD,连结AC交⊙O于点F,连接BE,DE,DF.
(1)若∠E=35°,求∠BDF的度数.
(2)若DF=4,cos∠CFD=![]() ,E是
,E是![]() 的中点,求DE的长.
的中点,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定,以二次函数y=ax2+bx+c的二次项系数a的2倍为一次项系数,一次项系数b为常数项构造的一次函数y=2ax+b叫做二次函数y=ax2+bx+c的“子函数”,反过来,二次函数y=ax2+bx+c叫做一次函数y=2ax+b的“母函数”.
(1)若一次函数y=2x-4是二次函数y=ax2+bx+c的“子函数”,且二次函数经过点(3,0),求此二次函数的解析式及顶点坐标.
(2)若“子函数”y=x-6的“母函数”的最小值为1,求“母函数”的函数表达式.
(3)已知二次函数y=-x2-4x+8的“子函数”图象直线l与x轴、y轴交于C、D两点,动点P为二次函数y=-x2-4x+8对称轴右侧上的动点,求△PCD的面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
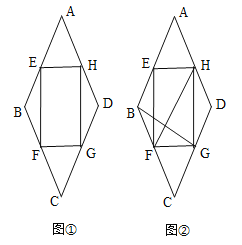
【题目】在菱形ABCD中,∠A=60°,AB=8cm,如图①,点E,H从点A开始向B,D运动,同时点F,G从点C向B,D运动,运动速度都为1cm/秒,运动时间为t秒(0≤t<8).
(1)当运动时间t=4时,求证:四边形EFGH为矩形;
(2)当t等于多少秒时,四边形EFGH面积是菱形ABCD面积的![]() ;
;
(3)如图②,连接HF,BG,当t等于多少秒时,HF⊥BG.
查看答案和解析>>
科目:初中数学 来源: 题型:
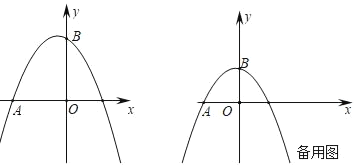
【题目】已知抛物线y=ax2﹣![]() x+c经过A(﹣2,0),B(0,2)两点,动点P,Q同时从原点出发均以1个单位/秒的速度运动,动点P沿x轴正方向运动,动点Q沿y轴正方向运动,连接PQ,设运动时间为t秒
x+c经过A(﹣2,0),B(0,2)两点,动点P,Q同时从原点出发均以1个单位/秒的速度运动,动点P沿x轴正方向运动,动点Q沿y轴正方向运动,连接PQ,设运动时间为t秒
(1)求抛物线的解析式;
(2)当BQ=![]() AP时,求t的值;
AP时,求t的值;
(3)随着点P,Q的运动,抛物线上是否存在点M,使△MPQ为等边三角形?若存在,请求出t的值及相应点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明、小军两同学做游戏,游戏规则是:一个不透明的文具袋中,装有型号完全相同的3支红笔和2支黑笔,两人先后从袋中取出一支笔(不放回),若两人所取笔的颜色相同,则小明胜,否则,小军胜.
(1)请用树形图或列表法列出摸笔游戏所有可能的结果;
(2)请计算小明获胜的概率,并指出本游戏规则是否公平,若不公平,你认为对谁有利.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+6x+c交x轴于A,B两点,交y轴于点C.直线y=x﹣5经过点B,C.
(1)求抛物线的解析式;
(2)过点A的直线交直线BC于点M.
①当AM⊥BC时,过抛物线上一动点P(不与点B,C重合),作直线AM的平行线交直线BC于点Q,若以点A,M,P,Q为顶点的四边形是平行四边形,求点P的横坐标;
②连接AC,当直线AM与直线BC的夹角等于∠ACB的2倍时,请直接写出点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com