
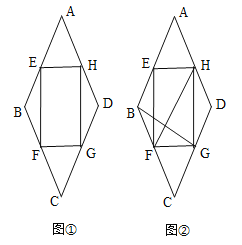
【题目】在菱形ABCD中,∠A=60°,AB=8cm,如图①,点E,H从点A开始向B,D运动,同时点F,G从点C向B,D运动,运动速度都为1cm/秒,运动时间为t秒(0≤t<8).
(1)当运动时间t=4时,求证:四边形EFGH为矩形;
(2)当t等于多少秒时,四边形EFGH面积是菱形ABCD面积的![]() ;
;
(3)如图②,连接HF,BG,当t等于多少秒时,HF⊥BG.
【答案】(1)见解析;(2) t=![]() ;(3)t=4.
;(3)t=4.
【解析】
(1)根据t=4时,E、F、G、H分别是AB、BC、CD、AD的中点,可证四边形EFGH为矩形;
(2)先证明四边形EFGH为矩形,然后根据∠ADB=60°求出HG=![]() ,由四边形EFGH面积是菱形ABCD面积的
,由四边形EFGH面积是菱形ABCD面积的![]() 列方程求解即可;
列方程求解即可;
(3)延长GF,过点B作BM⊥FG交点M,由(2)可知,FG=t, HG=![]() ,证明
,证明![]() ∽
∽![]() ,根据相似三角形的对应边成比例列出比例式,在含30°的直角三角形BMF中求出BM、FM,代入比例式即可求出t值.
,根据相似三角形的对应边成比例列出比例式,在含30°的直角三角形BMF中求出BM、FM,代入比例式即可求出t值.
解:(1)连接AC、BD,如图:
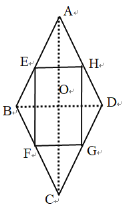
当t=4时,AE=AH=CF=CG=4
![]() 在菱形ABCD中,AB=BC=CD=AD=8,AC⊥BD
在菱形ABCD中,AB=BC=CD=AD=8,AC⊥BD
![]() E、F、G、H分别是AB、BC、CD、AD的中点
E、F、G、H分别是AB、BC、CD、AD的中点
![]() EH∥BD,FG∥BD,EF∥AC,HG∥AC
EH∥BD,FG∥BD,EF∥AC,HG∥AC
![]() EH∥FG,EF∥HG
EH∥FG,EF∥HG ![]() EH∥BD,FG∥BD
EH∥BD,FG∥BD
![]() 四边形EFGH为平行四边形
四边形EFGH为平行四边形
![]() EH∥BD,EF∥AC,AC⊥BD
EH∥BD,EF∥AC,AC⊥BD
![]() EH⊥RF
EH⊥RF
![]() 四边形EFGH为矩形;
四边形EFGH为矩形;
(2)由(1)中图可知AE=AH=CF=CG=t,则BE=DH=BF=DG=8-t
![]() 在菱形ABCD中,AB=BC=CD=AD=8,AC⊥BD,∠A=60°,
在菱形ABCD中,AB=BC=CD=AD=8,AC⊥BD,∠A=60°,
![]() EH=t,∠ADB=60°,
EH=t,∠ADB=60°,
![]() ,∠A=∠A ,
,∠A=∠A ,
![]()
![]()
![]()
![]()
![]() EH∥BD
EH∥BD
同理可得:FG∥BD,EF∥AC,HG∥AC,
![]() EH∥FG,EF∥HG,
EH∥FG,EF∥HG,
![]() EH∥BD,FG∥BD
EH∥BD,FG∥BD
![]() 四边形EFGH为平行四边形
四边形EFGH为平行四边形
![]() EH∥BD,EF∥AC,AC⊥BD,
EH∥BD,EF∥AC,AC⊥BD,
![]() EH⊥EF,
EH⊥EF,
![]() 四边形EFGH为矩形,
四边形EFGH为矩形,
![]() ∠ADB=60°,BD⊥HG,
∠ADB=60°,BD⊥HG,
![]() HG=
HG=![]()
![]() 四边形EFGH面积是菱形ABCD面积的
四边形EFGH面积是菱形ABCD面积的![]() ,
,
![]() t·
t·![]() =
=![]() ·
·![]() ·8·
·8·![]()
解得 t=![]() ,
,
![]() 当t=
当t=![]() 时,四边形EFGH面积是菱形ABCD面积的
时,四边形EFGH面积是菱形ABCD面积的![]() ;
;
(3)延长GF,过点B作BM⊥FG交点M,
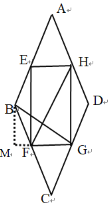
由(2)可知,FG=t,BF=8-t,HG=![]() ,四边形EFGH为矩形,HF⊥BG
,四边形EFGH为矩形,HF⊥BG
![]() ∠FHG+∠HFG=90°,∠FGB+∠HFG=90°
∠FHG+∠HFG=90°,∠FGB+∠HFG=90° ![]() ∠FHG=∠FGB
∠FHG=∠FGB
又∠FGH=∠FMB,
![]() ∽
∽![]()
![]() ,
,
![]()
![]()
![]()
![]()

化简得![]()
解得t=4或t=24(舍去)
![]() 当t=4时,HF⊥BG.
当t=4时,HF⊥BG.


 名师点拨卷系列答案
名师点拨卷系列答案科目:初中数学 来源: 题型:
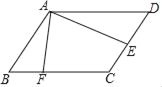
【题目】如图,在![]() ABCD中,点E为CD的中点,点F在BC上,且CF=2BF,连接AE,AF,若AF=
ABCD中,点E为CD的中点,点F在BC上,且CF=2BF,连接AE,AF,若AF=![]() ,AE=7,tan∠EAF=
,AE=7,tan∠EAF=![]() ,则线段BF的长为__________.
,则线段BF的长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
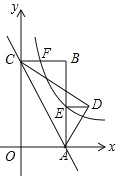
【题目】如图,矩形OABC的边OA,OC分别在x轴、y轴上,点B的坐标为(![]() ,5),△ACD与△ACO关于直线AC对称(点D和O对应),反比例函数y=
,5),△ACD与△ACO关于直线AC对称(点D和O对应),反比例函数y=![]() (k≠0)的图象与AB,BC分别交于E,F两点,连结DE,若DE∥x轴,则点F的坐标为_____.
(k≠0)的图象与AB,BC分别交于E,F两点,连结DE,若DE∥x轴,则点F的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将Rt△ABC绕直角顶点B逆时针旋转90°得到△DBE,DE的延长线恰好经过AC的中点F,连接AD,CE.
(1)求证:AE=CE;
(2)若BC=![]() ,求AB的长.
,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列几组勾股数:3,4,5; 5,12,13; 7,24,25; 9,40,41…按此规律,当直角三角形的最小直角边长是11时,则较长直角边长是________;当直角三角形的最小直角边长是![]() 时,则较长直角边长是________.
时,则较长直角边长是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+2x+3与x轴交于点A,C(点A在点C的右侧),与y轴交于点B
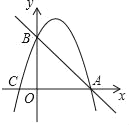
(1)求点A,B的坐标及直线AB的函数表达式;
(2)若直线l⊥x轴,且直线l在第一象限内与抛物线交于点M,与直线AB交于点N,求点M与点N之间的距离的最大值,并求出此时点M,N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A(m,2),B(﹣3,n)两点关于原点O对称,反比例函数y=![]() 的图象经过点A.
的图象经过点A.
(1)求反比例函数的解析式并判断点B是否在这个反比例函数的图象上;
(2)点P(x1,y1)也在这个反比例函数的图象上,﹣3<x1<m且x1≠0,请直接写出y1的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=kx+k﹣2经过点(m,n+1)和(m+1,2n+3),且﹣2<k<0,则n的取值范围是( )
A. ﹣2<n<0B. ﹣4<n<﹣2C. ﹣4<n<0D. 0<n<﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上),已知AB=80 m,DE=10 m,求障碍物B,C两点间的距离.(结果精确到0.1 m)(参考数据: ![]() ≈1.414,、
≈1.414,、![]() ≈1.732)
≈1.732)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com