
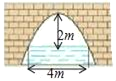
【题目】如图是抛物线型拱桥,当拱顶离水面2m时,水面宽4m.水面下降2.5m,水面宽度增加_____m.
【答案】2.
【解析】
根据已知建立平面直角坐标系,进而求出二次函数解析式,再通过把y=-2.5代入抛物线解析式得出水面宽度,即可得出答案
解:建立平面直角坐标系,设横轴x通过AB,纵轴y通过AB中点O且通过C点,则通过画图可得知O为原点,
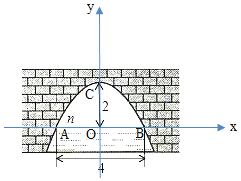
抛物线以y轴为对称轴,且经过A,B两点,OA和OB可求出为AB的一半2米,抛物线顶点C坐标为(0,2),
设顶点式y=ax2+2,把A点坐标(-2,0)代入得a=-0.5,
∴抛物线解析式为y=-0.5x2+2,
当水面下降2.5米,通过抛物线在图上的观察可转化为:
当y=-2.5时,对应的抛物线上两点之间的距离,也就是直线y=-1与抛物线相交的两点之间的距离,
可以通过把y=-2.5代入抛物线解析式得出:
-2.5=-0.5x2+2,
解得:x=±3,
2×3-4=2,
所以水面下降2.5m,水面宽度增加2米.
故答案为:2.


科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
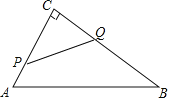
中,![]() ,AB=10cm,BC=8cm,点P从点A沿AC向点C以1cm/s的速度运动,同时点Q从点C沿CB向点B以2cm/s的速度运动(点Q运动到点B停止)。则四边形PABQ的面积y(
,AB=10cm,BC=8cm,点P从点A沿AC向点C以1cm/s的速度运动,同时点Q从点C沿CB向点B以2cm/s的速度运动(点Q运动到点B停止)。则四边形PABQ的面积y(![]() )与运动时间x(s)之间的函数图象为( )
)与运动时间x(s)之间的函数图象为( )
A. 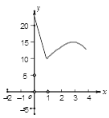 B.
B. 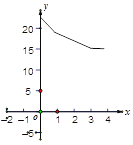
C.  D.
D. 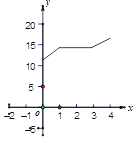
查看答案和解析>>
科目:初中数学 来源: 题型:
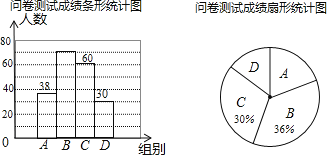
【题目】为了了解同学们对垃圾分类知识的了解程度,增强同学们的环保意识某校数学兴趣小组设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取若干名同学进行了问卷测试,根据测试成绩分布情况,将测试成绩分成A、B、C、D四组,绘制了如下统计图表
问卷测试成绩分组表
组别 | 分数/分 |
A | 60<x≤70 |
B | 70<x≤80 |
C | 80<x≤90 |
D | 90<x≤100 |
(1)本次抽样调查的样本总量是 ;
(2)样本中,测试成绩在B组的频数是 ,D组的频率是 ;
(3)样本中,这次测试成绩的中位数落在 组;
(4)如果该校共有880名学生,请估计成绩在90<x≤100的学生约有 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种商品的标价为500元/件,经过两次降价后的价格为405元/件,并且两次降价的百分率相同.
(1)求该种商品每次降价的百分率;
(2)若该种商品进价为400元/件,两次降价共售出此种商品100件,为使两次降价销售的总利润不少于3200元.问第一次降价后至少要售出该种商品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+2x+3与x轴交于点A,C(点A在点C的右侧),与y轴交于点B
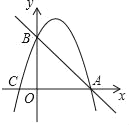
(1)求点A,B的坐标及直线AB的函数表达式;
(2)若直线l⊥x轴,且直线l在第一象限内与抛物线交于点M,与直线AB交于点N,求点M与点N之间的距离的最大值,并求出此时点M,N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
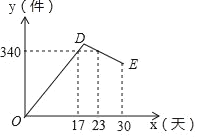
【题目】某公司开发出一款新的节能产品,该产品的成本价为6元件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试营销,售价为9元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘成图象,图中的折线ODE表示日销售量y(件)与销售时间x(天)之间的函数关系,已知线段DE表示的函数关系中,时间每增加1天,日销售量减少4件,
(1)请直接写出y与x之间的函数关系式;
(2)日销售利润不低于960元的天数共有多少天?试销售期间,日销售最大利润是多少元?
(3)工作人员在统计的过程中发现,有连续两天的销售利润之和为1980元,请你算出是哪两天.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在国家“一带一路”发展战略等多种因素影响下,某企业的利润逐年提高,据统计,该企业2016年利润为3亿元,2018年利润为4.32亿元,若2019年保持前两年的年平均增长率不变,该企业2019年利润能否超过5亿元?
查看答案和解析>>
科目:初中数学 来源: 题型:
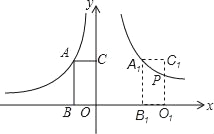
【题目】如图,在平面直角坐标系中,矩形ABOC的两边在坐标轴上,OB=1,点A在函数y=﹣![]() (x<0)的图象上,将此矩形向右平移3个单位长度到A1B1O1C1的位置,此时点A1在函数y=
(x<0)的图象上,将此矩形向右平移3个单位长度到A1B1O1C1的位置,此时点A1在函数y=![]() (x>0)的图象上,C1O1与此图象交于点P,则点P的纵坐标是( )
(x>0)的图象上,C1O1与此图象交于点P,则点P的纵坐标是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某数学兴趣小组在活动课上测量学校旗杆的高度.已知小亮站着测量,眼睛与地面的距离(AB)是1.7米,看旗杆顶部E的仰角为30°;小敏蹲着测量,眼睛与地面的距离(CD)是0.7米,看旗杆顶部E的仰角为45°.两人相距5米且位于旗杆同侧(点B、D、F在同一直线上).
(1)求小敏到旗杆的距离DF.(结果保留根号)
(2)求旗杆EF的高度.(结果保留整数,参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7)
≈1.7)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com