
【题目】为拓宽学生视野,我市某中学决定组织部分师生去庐山西海开展研学旅行活动,在参加此次活动的师生中,若每位老师带17个学生,还剩12个学生没人带;若每位老师带18个学生,就有一位老师少带4个学生.为了安全,既要保证所有师生都有车坐,又要保证每辆客车上至少要有2名老师.现有甲、乙两种大客车,它们的载客量和租金如表所示.
甲种客车 | 乙种客车 | |
载客量/(人/辆) | 30 | 42 |
租金/(元/辆) | 300 | 400 |
(1)参加此次研学旅行活动的老师和学生各有多少人?租用客车总数为多少辆?
(2)设租用x辆乙种客车,租车总费用为w元,请写出w与x之间的函数关系式;
(3)在(2)的条件下,学校计划此次研学旅行活动的租车总费用不超过3100元,租用乙种客车不少5辆,你能得出哪几种不同的租车方案?其中哪种租车方案最省钱?请说明理由.
【答案】(1)老师有16名,学生有284名;租用客车总数为8辆;(2)w=100x+2400;(3)共有3种租车方案:①租用甲种客车3辆,乙种客车5辆,租车费用为2900元;②租用甲种客车2辆,乙种客车6辆,租车费用为3000元;③租用甲种客车1辆,乙种客车7辆,租车费用为3100元;最节省费用的租车方案是:租用甲种客车3辆,乙种客车5辆.
【解析】
(1)设出老师有x名,学生有y名,得出二元一次方程组,解出即可;再由每辆客车上至少要有2名老师,且要保证300名师生有车坐,可得租用客车总数;
(2)由租用x辆乙种客车,得甲种客车数为:(8﹣x)辆,由题意得出w=400x+300(8﹣x)即可;
(3)由题意得出400x+300(8﹣x)≤3100,且x≥5,得出x取值范围,分析得出即可.
解:(1)设老师有x名,学生有y名.
依题意,列方程组![]() ,
,
解得:![]() ,
,
∵每辆客车上至少要有2名老师,
∴汽车总数不能超过8辆;
又要保证300名师生有车坐,汽车总数不能小于![]() (取整为8)辆,
(取整为8)辆,
综合起来可知汽车总数为8辆;
答:老师有16名,学生有284名;租用客车总数为8辆.
(2)∵租用x辆乙种客车,
∴甲种客车数为:(8﹣x)辆,
∴w=400x+300(8﹣x)=100x+2400.
(3)∵租车总费用不超过3100元,租用乙种客车不少于5辆,
∴400x+300(8﹣x)≤3100,x≥5
解得:5≤x≤7,
为使300名师生都有座,
∴42x+30(8﹣x)≥300,
解得:x≥5,
∴5≤x≤7,(x为整数),
∴共有3种租车方案:
方案一:租用甲种客车3辆,乙种客车5辆,租车费用为2900元;
方案二:租用甲种客车2辆,乙种客车6辆,租车费用为3000元;
方案三:租用甲种客车1辆,乙种客车7辆,租车费用为3100元;
故最节省费用的租车方案是:租用甲种客车3辆,乙种客车5辆.


科目:初中数学 来源: 题型:
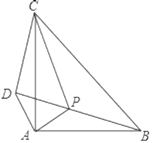
【题目】如图所示,在等腰Rt△ABC中,∠CAB=90°,P是△ABC内一点,将△PAB绕A逆时针旋转90°得△DAC.
(1)试判断△PAD的形状并说明理由;
(2)连接PC,若∠APB=135°,PA=1,PB=3,求PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
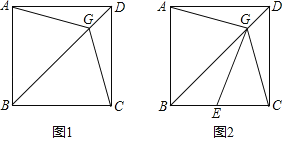
【题目】(1)如图1,在矩形ABCD中,对角线AC与BD相交于点O,过点O作直线EF⊥BD,且交AD于点E,交BC于点F,连接BE,DF,且BE平分∠ABD.
①求证:四边形BFDE是菱形;
②直接写出∠EBF的度数.
(2)把(1)中菱形BFDE进行分离研究,如图2,G,I分别在BF,BE边上,且BG=BI,连接GD,H为GD的中点,连接FH,并延长FH交ED于点J,连接IJ,IH,IF,IG.试探究线段IH与FH之间满足的关系,并说明理由;
(3)把(1)中矩形ABCD进行特殊化探究,如图3,矩形ABCD满足AB=AD时,点E是对角线AC上一点,连接DE,作EF⊥DE,垂足为点E,交AB于点F,连接DF,交AC于点G.请直接写出线段AG,GE,EC三者之间满足的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一道作业题:
(1)请你完成这道题的证明;
已知:如图1,在正方形ABCD中,G是对角线BD上一点(G与B,D不重合)连结AG,CG
求证:△BAG≌△BCG
(2)做完(1)后,小颖善于反思,她又提出了如下的问题,请你解答.
如果在射线CB上取点E,使GE=GC,连结GE.
①如图2,当点E在线段CB上时,求证:AG⊥EG.
②探究线段AB,BE,BG之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为更精准地关爱留守学生,某学校将留守学生的各种情形分成四种类型:A.由父母一方照看;B.由爷爷奶奶照看;C.由叔姨等近亲照看;D.直接寄宿学校.某数学小组随机调查了一个班级,发现该班留守学生数量占全班总人数的20%,并将调查结果制成如下两幅不完整的统计图.
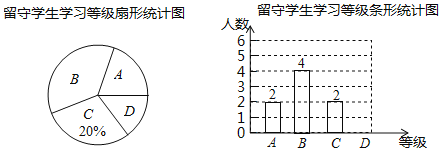
(1)该班共有 名留守学生,B类型留守学生所在扇形的圆心角的度数为 ;
(2)将条形统计图补充完整;
(3)已知该校共有2400名学生,现学校打算对D类型的留守学生进行手拉手关爱活动,请你估计该校将有多少名留守学生在此关爱活动中受益?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的边AB为直径作⊙O,与BC交于点D,点E是弧BD的中点,连接AE交BC于点F,∠ACB=2∠BAE.
(1)求证:AC是⊙O的切线;
(2)若![]() ,BD=5,求BF的长.
,BD=5,求BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
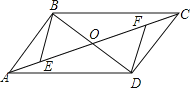
【题目】如图,ABCD的对角线AC、BD相交于点O,OE=OF.
(1)求证:△BOE≌△DOF;
(2)若BD=EF,连接DE、BF,判断四边形EBFD的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段 AB 经过⊙O 的圆心, AC , BD 分别与⊙O 相切于点 C ,D .若 AC =BD = 4 ,∠A=45°,则弧CD的长度为( )
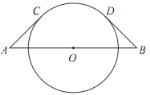
A.πB.2πC.2![]() πD.4π
πD.4π
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com