
【题目】如图,以△ABC的边AB为直径作⊙O,与BC交于点D,点E是弧BD的中点,连接AE交BC于点F,∠ACB=2∠BAE.
(1)求证:AC是⊙O的切线;
(2)若![]() ,BD=5,求BF的长.
,BD=5,求BF的长.

【答案】(1)证明见解析;(2)3.
【解析】试题分析:(1)连接AD,由圆周角定理得出∠1=∠2.证出∠C=∠BAD.由圆周角定理证出∠DAC+∠BAD=90°,得出∠BAC=90°,即可得出结论.
(2)过点F作FG⊥AB于点G.由三角函数得出sinB=![]() ,设AD=2m,则AB=3m,由勾股定理求出BD=
,设AD=2m,则AB=3m,由勾股定理求出BD=![]() m.求出m=
m.求出m=![]() .得出AD=2
.得出AD=2![]() ,AB=3
,AB=3![]() .证出FG=FD.设BF=x,则FG=FD=5-x.由三角函数得出方程,解方程即可.
.证出FG=FD.设BF=x,则FG=FD=5-x.由三角函数得出方程,解方程即可.
试题解析:(1)证明:连接AD.

∵ E是弧BD的中点,∴弧BE = 弧ED,∴∠BAD=2∠BAE.
∵![]()
∵AB为⊙O直径, ∴∠ADB=90°,∴∠DAC+∠ACB =90°.
∴∠BAC =∠DAC+∠BAD =90°.
∴AC是⊙O的切线.
(2)解:过点F作FG⊥AB于点G.
∵∠BAE=∠DAE,∠ADB=90°,∴GF=DF.
在Rt△BGF中,∠BGF=90°,![]()
设BF=x,则GF=5-x,∴![]() ,x=3,即BF=3.
,x=3,即BF=3.


科目:初中数学 来源: 题型:
【题目】某市公交公司为应对春运期间的人流高峰,计划购买A、B两种型号的公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车3辆,共需650万元,
(1)试问该公交公司计划购买A型和B型公交车每辆各需多少万元?
(2)若该公司预计在某条线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用W不超过1200万元,且确保这10辆公交车在某条线路的年均载客量总和不少于680万人次,则该公司有哪几种购车方案?哪种购车方案的总费用W最少?最少总费用是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A. 当AB=BC时,它是菱形 B. 当AC⊥BD时,它是菱形
C. 当∠ABC=90°时,它是矩形 D. 当AC=BD时,它是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究规律:如图,已知直线m∥n,A、B为直线n上的两点,C、P为直线m上的两点. 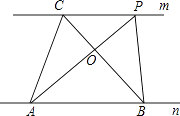
(1)请写出图中面积相等的各对三角形: .
(2)如果A、B、C为三个定点,点P在m上移动,那么无论P点移动到任何位置总有:与△ABC的面积相等;理由是: .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com