
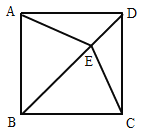
【题目】如图,在正方形ABCD中,E是对角线BD上一点,连接AE,CE.
(1)求证:AE=CE;
(2)若BC=![]() ,BE=6,求tan∠BAE的值.
,BE=6,求tan∠BAE的值.
 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
【题目】为拓宽学生视野,我市某中学决定组织部分师生去庐山西海开展研学旅行活动,在参加此次活动的师生中,若每位老师带17个学生,还剩12个学生没人带;若每位老师带18个学生,就有一位老师少带4个学生.为了安全,既要保证所有师生都有车坐,又要保证每辆客车上至少要有2名老师.现有甲、乙两种大客车,它们的载客量和租金如表所示.
甲种客车 | 乙种客车 | |
载客量/(人/辆) | 30 | 42 |
租金/(元/辆) | 300 | 400 |
(1)参加此次研学旅行活动的老师和学生各有多少人?租用客车总数为多少辆?
(2)设租用x辆乙种客车,租车总费用为w元,请写出w与x之间的函数关系式;
(3)在(2)的条件下,学校计划此次研学旅行活动的租车总费用不超过3100元,租用乙种客车不少5辆,你能得出哪几种不同的租车方案?其中哪种租车方案最省钱?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
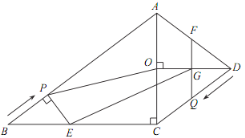
【题目】已知:如图,在四边形 ABCD 中, AB∥CD, ACB =90°, AB=10cm, BC=8cm, OD 垂直平分 A C.点 P 从点 B 出发,沿 BA 方向匀速运动,速度为 1cm/s;同时,点 Q 从点 D 出发,沿 DC 方向匀速运动,速度为 1cm/s;当一个点停止运动,另一个点也停止运动.过点 P作 PE⊥AB,交 BC 于点 E,过点 Q 作 QF∥AC,分别交 AD, OD 于点 F, G.连接 OP,EG.设运动时间为 t ( s )(0<t<5) ,解答下列问题:
(1)当 t 为何值时,点 E 在 BAC 的平分线上?
(2)设四边形 PEGO 的面积为 S(cm2) ,求 S 与 t 的函数关系式;
(3)在运动过程中,是否存在某一时刻 t ,使四边形 PEGO 的面积最大?若存在,求出t 的值;若不存在,请说明理由;
(4)连接 OE, OQ,在运动过程中,是否存在某一时刻 t ,使 OE⊥OQ?若存在,求出t 的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
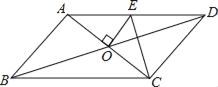
【题目】如图,平行四边形ABCD的对角线相交于点O,且AD>AB,过点O作OE⊥AC交AD于点E,连接CE.若平行四边形ABCD的周长为20,则△CDE的周长是( )
A. 10B. 11C. 12D. 13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AD是△ABC的中线P是线段AD上的一点(不与点A、D重合),连接PB、PC,E、F、G、H分别是AB、AC、PB、PC的中点,AD与EF交于点M;
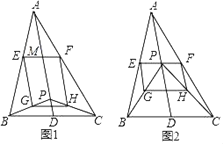
(1)如图1,当AB=AC时,求证:四边形EGHF是矩形;
(2)如图2,当点P与点M重合时,在不添加任何辅助线的条件下,写出所有与△BPE面积相等的三角形(不包括△BPE本身).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年永州市初中体育水平测试进行改革,增加了自选项目,学生可以从篮球运球、足球运球、排球向上垫球三项中必须选一项,另外从一分钟跳绳、仰卧起坐(女)或引体向上(男)、原地正面掷实心球、立定跳远中必须选一项.现对永州市某校的选考项目情况进行调查,对调查结果进行了分析统计并制作了两幅统计图:
项目 | 篮球 | 足球 | 排球 | |||
性别 | 男 | 女 | 男 | 女 | 男 | 女 |
人数 | 30 | 10 | 24 | 12 | 6 | 28 |
平均得分 | 8 | 7 | 8.5 | 6 | 9 | 10 |
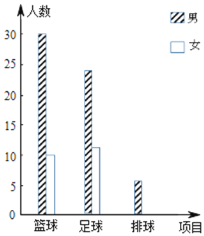
(1)补全条形统计图;
(2)求抽查的这些男生的体育测试平均分;
(3)若该校准备从这次体育测试成绩好的学生中选出10名参加全市运动会.现在有19名学生报名,小明是这19名同学之一,小明在知道自己这次成绩后还需知道这19名学生成绩的______,就能知道自己能不能参加市运动会.
A.平均数B.众数C.中位数D.方差
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有一组数据:165、160、166、170、164、165,若去掉最后一个数165,下列说法正确的是( )
A. 平均数不变,方差变大B. 平均数不变,方差不变
C. 平均数不变,方差变小D. 平均数变小,方差不变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H.给出下列结论:①BE=2AE;②△DFP~△BPH;③![]() ;④DP2=PHPC;其中正确的是( )
;④DP2=PHPC;其中正确的是( )
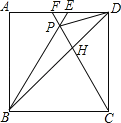
A. ①②③④B. ①③④C. ②③D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知P(x1,y1)Q(x2,y2),定义P、Q两点的横坐标之差的绝对值与纵坐标之差的绝对值的和为P、Q两点的直角距离,记作d(P,Q).即d(P,Q)=|x2﹣x1|+|y2﹣y1|
如图1,在平面直角坐标系xOy中,A(1,4),B(5,2),则d(A,B)=|5﹣1|+|2﹣4|=6.
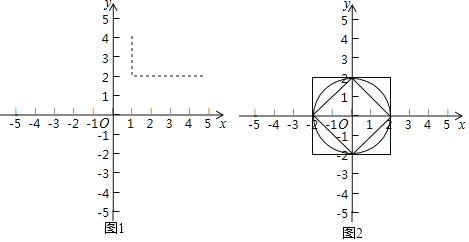
(1)如图2,已知以下三个图形:
①以原点为圆心,2为半径的圆;
②以原点为中心,4为边长,且各边分别与坐标轴垂直的正方形;
③以原点为中心,对角线分别在两条坐标轴上,对角线长为4的正方形.
点P是上面某个图形上的一个动点,且满足d(O,P)=2总成立.写出符合题意的图形对应的序号 .
(2)若直线y=k(x+3)上存在点P使得d(O,P)=2,求k的取值范围.
(3)在平面直角坐标系xOy中,P为动点,且d(O,P)=3,⊙M圆心为M(t,0),半径为1.若⊙M上存在点N使得PN=1,求t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com